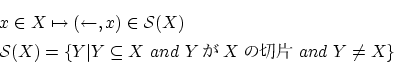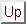


: 整列可能定理
: 整列順序
: 整列順序の定義
目次
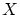 が整列集合とし,
が整列集合とし,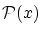 は関係式とします。
は関係式とします。
が成立つとき
が成立ちます。これを自然数での数学的帰納法になぞらえて超限帰納法と呼びます。
[証明]
前半の関係式
が成立してかつ
が成立たないとします。
ですから
が成立ち,集合
が空集合でないことになります。
すると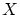 は整列集合でしたから
は整列集合でしたから
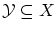 には最小元
には最小元
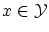 が存在します。
が存在します。
しかし,任意の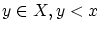 については
については
 ゆえ,
ゆえ,
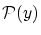 が成立します。すると仮定した前半の関係式から,
が成立します。すると仮定した前半の関係式から,
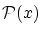 が成立ちこれは
が成立ちこれは
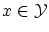 に矛盾します。
[証明終]
に矛盾します。
[証明終]
順序集合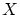 で,
で,
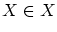 について
について
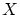 を整列順序集合とするとき:
を整列順序集合とするとき:
[証明]
-
とすると:
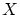 は整列順序集合だから
は整列順序集合だから
が存在する。
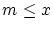 のとき,
のとき,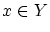 とすると
とすると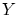 が
が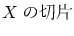 だから
だから
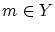 となり,矛盾。よって
となり,矛盾。よって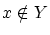
よって,
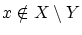 とすると
とすると
よって
ゆえに,
- 逆に,
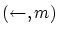 が
が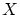 の切片で
の切片で
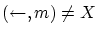 は明らか。
は明らか。
[証明終]
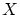 を整列順序集合とするとき:
を整列順序集合とするとき:
は整列順序について同型。
は整列順序集合
[証明]
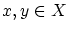 を任意にとるとき,
を任意にとるとき,
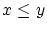 から
から
で
従って
-
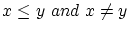 のとき
のとき
とすると
から
よって
となり矛盾。よって,
従って
よって
は整列順序について同型。
が整列順序集合であることも明らか。(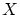 を最大元として
を最大元として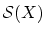 に加える。)
に加える。)



: 整列可能定理
: 整列順序
: 整列順序の定義
目次
Yasunari SHIDAMA
![]() が整列集合とし,
が整列集合とし,![]() は関係式とします。
は関係式とします。
![]() については
については
![]() ゆえ,
ゆえ,
![]() が成立します。すると仮定した前半の関係式から,
が成立します。すると仮定した前半の関係式から,
![]() が成立ちこれは
が成立ちこれは
![]() に矛盾します。
[証明終]
に矛盾します。
[証明終]
![]() で,
で,
![]() について
について
![]() を整列順序集合とするとき:
を整列順序集合とするとき:
![]() のとき,
のとき,![]() とすると
とすると![]() が
が![]() だから
だから
![]() となり,矛盾。よって
となり,矛盾。よって![]()
![]() とすると
とすると
![]() を整列順序集合とするとき:
を整列順序集合とするとき:
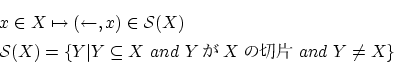
![]() から
から