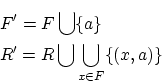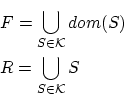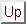


: Zrnの補題
: 整列順序
: 超限帰納法
目次
以下の定理が知られています。
[ツェルメロの整列可能性定理]
任意の集合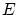 上に整列順序が存在する。
上に整列順序が存在する。
以下に証明を述べますが,
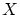 が有限集合か,自然数の集合
が有限集合か,自然数の集合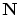 との間に双射が存在するなら整列順序を入れることは
難しくありません。実際,双射
との間に双射が存在するなら整列順序を入れることは
難しくありません。実際,双射
があれば,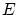 の順序を
の順序を
で定義すればこの順序関係は整列順序になります。ただし,この資料では,第5章で集合の
基数を定義して,それによって始めて自然数が定義されます。
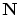 との間に双射が存在しなくても,順序を定義する方法の,アイデアの一つは,次のようなものです。
との間に双射が存在しなくても,順序を定義する方法の,アイデアの一つは,次のようなものです。
まず,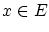 を一つ取り出し,これを定義したい順序で,最初の要素とします。
次に
を一つ取り出し,これを定義したい順序で,最初の要素とします。
次に
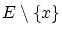 から要素
から要素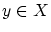 を取り出し,これを
を取り出し,これを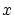 の次の要素とします。さらに
の次の要素とします。さらに
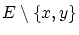 から要素
から要素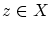 を取り出し,これを
を取り出し,これを の次の要素とします。無論は
の次の要素とします。無論は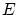 は無限集合で,しかも,
は無限集合で,しかも,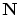 との間に双射が定義されず,1番目,2番目,…,と要素の選択を「数学的帰納法」で定義できないかもしれません。
との間に双射が定義されず,1番目,2番目,…,と要素の選択を「数学的帰納法」で定義できないかもしれません。
そこで,任意の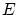 部分集合
部分集合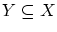 に対して,
に対して,
となるような写像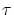 を作ります。このような写像は,
を作ります。このような写像は,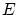 のべき集合
のべき集合
を使って造られる集合の族,
の多重直積
の元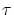 を使います。この集合が空集合でないことは,
を使います。この集合が空集合でないことは,
ですので選択公理によって保証されます。
の直感的な意味は,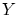 の全ての要素により(順序
の全ての要素により(順序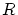 について)真に大きい要素で,しかもそのような要素の中では,一番小さい要素です。
結局
について)真に大きい要素で,しかもそのような要素の中では,一番小さい要素です。
結局
を使って,順序が定義される区間を漸次拡張する方法を使うことになりますが,
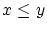 のとき
のとき
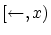 と
と
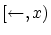 に定義された順序が矛盾の無いように定義していく必要があります。
に定義された順序が矛盾の無いように定義していく必要があります。
[ツェルメロの定理の証明]
上に述べたように,
とすると
であり,選択公理によって
その多重直積
は空集合ではない。この集合の元の一つを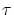 とすると,
とすると,
ここで,以下の補題を使えば
が成立ち,
だったので,
です。
[ツェルメロの定理の証明終]
[補題]
このとき
[補題の証明]
とおく。
ここで,
とおくと:
-
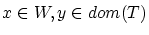 を任意にとり,
を任意にとり,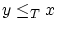 とすると
とすると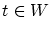 よって
よって
-
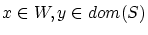 を任意にとり,
を任意にとり,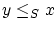 とすると
とすると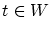 よって
よって
- また
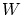 の構成法から
の構成法から
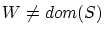 かつ
かつ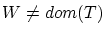 とすると
とすると
とおくと,
しかし,
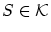 から
から
同様に,
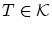 から
から
よって
ゆえに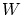 の定義から
の定義から
これは
に矛盾。
以上から
任意の
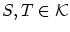 について
について
で
ここで,
とおくと:
-
- 任意の
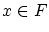 について,
について,
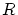 の作り方から
の作り方から
-
とすると,
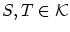 が存在して
が存在して
が成立ち,
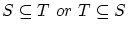 から
から
従って,
どちらの場合でも
-
とすると,上と全く同様に
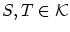 が存在して
が存在して
どちらの場合でも
- 任意の
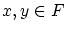 について,
について,
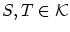 が存在して
が存在して
これについても
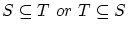 から
から
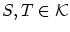 は整列順序ゆえ全順序でもあるので
は整列順序ゆえ全順序でもあるので
または
どちらにしても,
結局,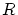 は
は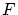 上の全順序になる。
上の全順序になる。
を任意にとると:
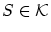 が存在して
が存在して
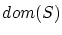 は整列集合で,
は整列集合で,
から,
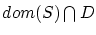 には最小元
には最小元
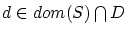 が存在する。
が存在する。
ここで,任意の
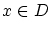 について
について
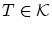 が存在して
が存在して
で,
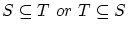 から
から
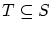 のときは
のときは
より,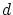 は
は
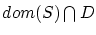 の
の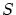 による最小元なので,
による最小元なので,
これから
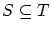 のときは
のときは
従って,
とすると,
しかし,これは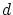 は
は
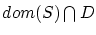 の
の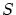 による最小元であることに矛盾
による最小元であることに矛盾
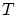 は全順序だったので
は全順序だったので
これから
結局,
ここで,任意の
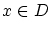 について
について
以上から,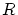 は
は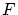 上の整列順序になっている。
上の整列順序になっている。
ここで,
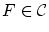 とすると,
とすると,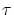 についての仮定から
についての仮定から
であり,
とおけば,
構成の仕方から,
にも関わらず,
でこれは
に矛盾する。
[補題の証明終]

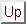


: Zrnの補題
: 整列順序
: 超限帰納法
目次
Yasunari SHIDAMA
![]() 上に整列順序が存在する。
上に整列順序が存在する。
![]() が有限集合か,自然数の集合
が有限集合か,自然数の集合![]() との間に双射が存在するなら整列順序を入れることは
難しくありません。実際,双射
との間に双射が存在するなら整列順序を入れることは
難しくありません。実際,双射
![]() との間に双射が存在しなくても,順序を定義する方法の,アイデアの一つは,次のようなものです。
との間に双射が存在しなくても,順序を定義する方法の,アイデアの一つは,次のようなものです。
![]() を一つ取り出し,これを定義したい順序で,最初の要素とします。
次に
を一つ取り出し,これを定義したい順序で,最初の要素とします。
次に
![]() から要素
から要素![]() を取り出し,これを
を取り出し,これを![]() の次の要素とします。さらに
の次の要素とします。さらに
![]() から要素
から要素![]() を取り出し,これを
を取り出し,これを![]() の次の要素とします。無論は
の次の要素とします。無論は![]() は無限集合で,しかも,
は無限集合で,しかも,![]() との間に双射が定義されず,1番目,2番目,…,と要素の選択を「数学的帰納法」で定義できないかもしれません。
との間に双射が定義されず,1番目,2番目,…,と要素の選択を「数学的帰納法」で定義できないかもしれません。
![]() 部分集合
部分集合![]() に対して,
に対して,
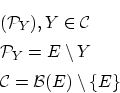
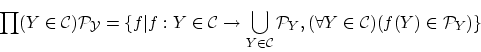
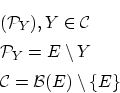
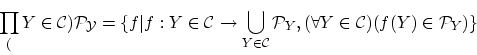
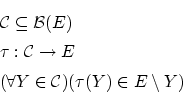
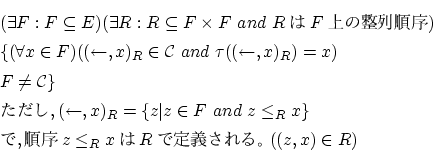

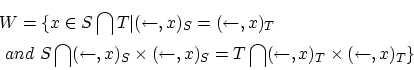
![]() について
について
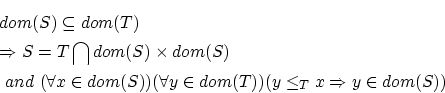
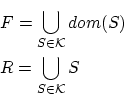
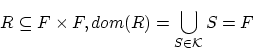
![]() の作り方から
の作り方から

![]() は
は![]() 上の全順序になる。
上の全順序になる。
![]() は整列集合で,
は整列集合で,
![]() について
について
![]() が存在して
が存在して
![]() は
は![]() 上の整列順序になっている。
上の整列順序になっている。
![]() とすると,
とすると,![]() についての仮定から
についての仮定から