
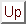


: 商集合
: 関係
: 同値関係
目次
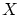 上の同値関係
上の同値関係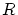 について,
について,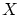 の元
の元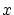 と同値な
と同値な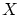 の元
の元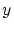 全体の集合を
全体の集合を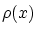 で表します.
で表します.
これを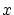 の同値類と呼びます.
このとき
の同値類と呼びます.
このとき
[証明]
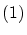
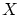 の元
の元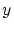 を任意にとり
を任意にとり
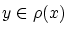 とすれば,
とすれば,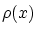 の定義から
の定義から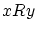 となる。
逆に
となる。
逆に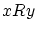 なら定義により
なら定義により
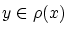
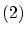
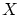 の元
の元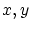 を任意にとると,
を任意にとると,
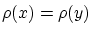 とすると
とすると
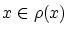 から
から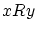
逆に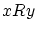 として
として
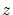 を任意にとって
を任意にとって
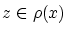 とすると
とすると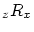 ゆえ,これと
ゆえ,これと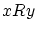 から
から
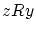 従って
従って
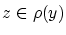
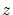 は任意にとったから
は任意にとったから
よって
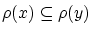
同様にして
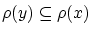 も得られるので,
も得られるので,
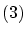
 の元
の元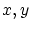 を任意にとると,
を任意にとると,
なら
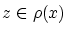 and
and
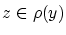 から
から
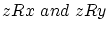 が得られ,
が得られ,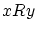
逆に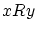 なら
なら 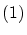 から
から
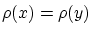 従って
従って
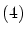 任意の
任意の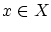
について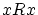 ですから,
ですから,
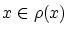
よって
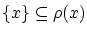
一方
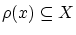 ですから
ですから
結局
[証明終り]
問題
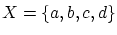 とするとき
とするとき
は同値関係の例です.
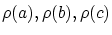 を求めてください.
を求めてください.
Yasunari SHIDAMA
![]() の同値類と呼びます.
このとき
の同値類と呼びます.
このとき
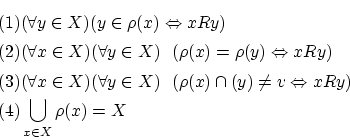
![]()
![]() も得られるので,
も得られるので,
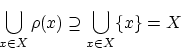
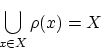
![]() とするとき
とするとき