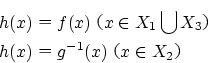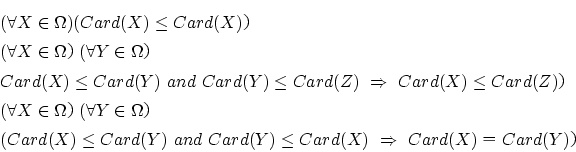定義から から
から への単射
への単射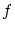 と
と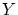 から
から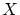 への単射
への単射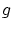 が存在します.
が存在します.
このとき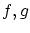 のうちどちらかが双射なら
のうちどちらかが双射なら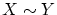
すなわち
となります.
以下のようにして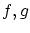 から
から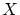 から
から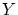 への双射を作り出します.
への双射を作り出します.
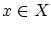 を任意に選びます.
を任意に選びます.
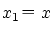 とおき,次のようにして
とおき,次のようにして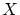 または
または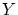 の
元の列
の
元の列
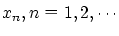 を構成します.
を構成します.
-
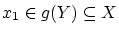 なら
なら 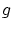 による逆像
による逆像
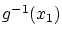 がありますので
がありますので
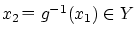
-
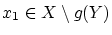 なら
なら 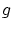 による逆像
による逆像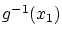 が存在しないので
が存在しないので
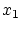 でこの列の作成手続きは終了
でこの列の作成手続きは終了
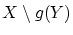 は
は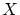 から
から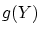 の要素を取り除いた集合です.
の要素を取り除いた集合です.
-
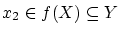 なら
なら 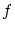 による逆像
による逆像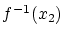 がありますので
がありますので
-
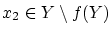 なら
なら 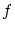 による逆像
による逆像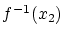 が存在しないので
が存在しないので
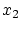 でこの列の作成手続きは終了.
でこの列の作成手続きは終了.
この手続きを繰り返します.
さて,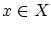 から出発して
から出発して
というように列
 が作られて行くわけですが
が作られて行くわけですが
最初の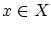 の取り方によって,
の取り方によって,
- (1)
 が無限の列になる。(手続きが無限に繰り
返される)
が無限の列になる。(手続きが無限に繰り
返される)
- (2)
 が奇数個の有限の列になる。(手続きが奇
数回目で終了)
が奇数個の有限の列になる。(手続きが奇
数回目で終了)
- (3)
 が偶数個の有限の列になる。(手続きが偶
数回目で終了)
が偶数個の有限の列になる。(手続きが偶
数回目で終了)
のどれかになります.
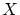 を(1),(2),(3)の場合によって分割します.
を(1),(2),(3)の場合によって分割します.
まったく同様の議論により
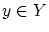 を選び
を選び
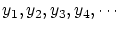 をることが可能で
をることが可能で
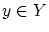 から出発して
から出発して
というように列が作られて行くわけですが
最初の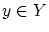 の取り方によって,
の取り方によって,
- (1')
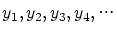 が無限の列になる。(手続きが無限に繰り返
が無限の列になる。(手続きが無限に繰り返
される)
- (2')
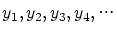 が奇数個の有限の列になる。(手続きが奇数
が奇数個の有限の列になる。(手続きが奇数
回目で終了)
- (3')
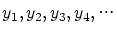 が偶数個の有限の列になる。(手続きが偶数
が偶数個の有限の列になる。(手続きが偶数
回目で終了)
のどれかになります.
 を(1'),(2'),(3')の場合によって分割します.
を(1'),(2'),(3')の場合によって分割します.
すると
 の任意の元
の任意の元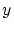 に対して必ず
に対して必ず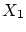 の元
の元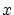 が存在して
が存在して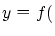 x
x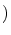 となります.
このような元が存在しなければ
となります.
このような元が存在しなければ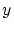 は
は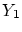 の元ではないことになります.
の元ではないことになります.
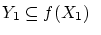 また,
また,
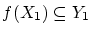 も成り立ちます.
も成り立ちます.
従って,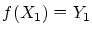 となります.
となります.
が成り立ちますので,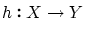 を
を
で定義すると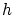 は
は
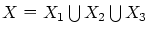 から
から
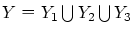 への双射になります.
への双射になります.
よって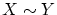 すなわち
すなわち
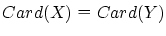 が成り立ちます.
が成り立ちます.
以上から,
証明終り
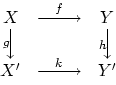
![]() は
は![]() から
から![]() への単射になります.
への単射になります.
![]() から出発して
から出発して
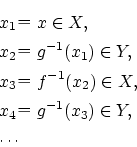
![]() が作られて行くわけですが
が作られて行くわけですが
![]() の取り方によって,
の取り方によって,
![]() を(1'),(2'),(3')の場合によって分割します.
を(1'),(2'),(3')の場合によって分割します.