


: 基数の集合の整列性
: 集合の基数
: 基数の順序関係
目次
さらに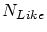 はこの順序
はこの順序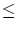 で全順序集合になります.
で全順序集合になります.
すなわち
これを証明するのには,直感的には以下の議論を行います.
- (1)
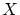 から元一個を取りだし
から元一個を取りだし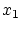 とします.次に
とします.次に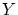 から元一個を取りだし
から元一個を取りだし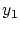 とします.
とします.
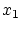 に
に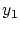 を対応させる写像を
を対応させる写像を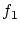 とします。
とします。 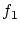 は
は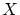 の要素一個だけからなる部分集合
の要素一個だけからなる部分集合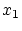 から
から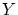 の要素一個だけからなる部分集合
の要素一個だけからなる部分集合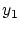 への双射です.
への双射です.
- (2) 次に,
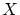 から
から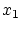 を取り去った残りの集合から別の元
を取り去った残りの集合から別の元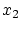 を取り出します.さらに
を取り出します.さらに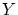 から
から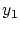 を取り去った残りの集合から別の元
を取り去った残りの集合から別の元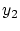 を取り出します.
を取り出します.
そして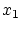 に
に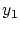 を,
を,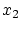 に
に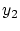 を対応させる写像を
を対応させる写像を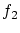 とします.
とします.
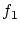 は
は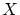 の要素2個だけからなる部分集合
の要素2個だけからなる部分集合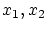 から
から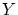 の要素2個だけからなる部分集合
の要素2個だけからなる部分集合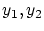 への双射です.
への双射です.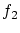 は
は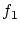 を拡張したことになります.
を拡張したことになります.
- (3) こうして,
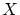 と
と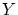 から順次要素を一個づつ取りだし,写像を拡張して行けば
から順次要素を一個づつ取りだし,写像を拡張して行けば
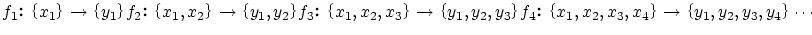
という,双射の列ができますが,この手続きは,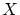 の要素が尽きるか,
の要素が尽きるか,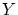 の要素が尽きるかによって止まるはずです.
の要素が尽きるかによって止まるはずです.
以上の手続きで先に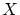 の要素が尽きればそのとき
の要素が尽きればそのとき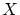 から
から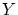 への単射が作られていることになり
への単射が作られていることになり
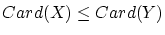 で逆に,
で逆に,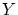 の要素が尽きれば
の要素が尽きれば
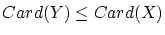 です.
です.
しかし,そもそもこの議論は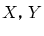 の要素が
の要素が
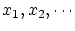 や
や
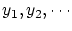 と番号付けできることを前提にしていますが(数学的帰納法を使うには添え字は自然数でなければならない)、例えば実数の集合の元にはそのような番号付けは出来ません.
と番号付けできることを前提にしていますが(数学的帰納法を使うには添え字は自然数でなければならない)、例えば実数の集合の元にはそのような番号付けは出来ません.
そこで定義域が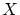 の部分集合で,値域が
の部分集合で,値域が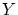 の部分集合である双射全体の集合
の部分集合である双射全体の集合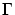 を考え,その
を考え,その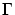 の任意の元
の任意の元
に順序を
で定義してこの順序での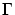 の極大元が存在することを示す方法が考えられます.それを可能にするのが以下の
の極大元が存在することを示す方法が考えられます.それを可能にするのが以下の
 です.
です.
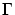 を順序関係が与えられた空でない集合とします.
を順序関係が与えられた空でない集合とします.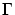 に極大元が存在するかどうかを判定するのに以下の
に極大元が存在するかどうかを判定するのに以下の
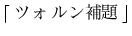 が知られています.
が知られています.
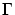 の任意の全順序部分集合
の任意の全順序部分集合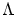 をとるとき,これが
をとるとき,これが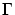 で常に上に有界であるとする.
このとき
で常に上に有界であるとする.
このとき には極大元が存在する.
には極大元が存在する.
これは,数学的帰納法で,
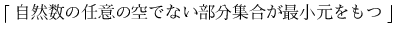 という自然数の集合の整列性を用いましたがこれに相当するものです.
という自然数の集合の整列性を用いましたがこれに相当するものです.
この補題は選択公理から証明できますが,ここでは省略します.
このツォルン補題を用いて,
すなわち,任意の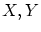 の間には
の間には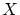 から
から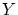 へか,あるいは
へか,あるいは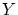 から
から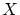 への双射が存在することをを証明します.
への双射が存在することをを証明します.
このために
定義域が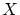 の部分集合で,値域が
の部分集合で,値域が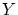 の部分集合である双射全体の集合
の部分集合である双射全体の集合
を考え,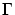 の任意の元
の任意の元
に順序を
で定義します.
問題5.2
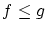 が
が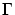 上の順序関係を定義していることを示して下さい.
上の順序関係を定義していることを示して下さい.
さて,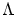 を
を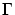 の任意の部分集合とし,順序
の任意の部分集合とし,順序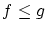 に関して,全順序部分集合とします.
に関して,全順序部分集合とします.
すなわち,
このとき
問題
と置くと
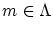 であり,
であり,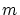 は
は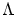 の
の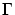 での上界
での上界
であることを示して下さい.
問題とツォルン補題によって,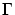 は極大元
は極大元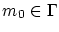 をもちます.
をもちます.
このとき
問題
が成り立っていることを示して下さい.
(ヒント:
背理法によります.
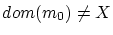 かつ
かつ
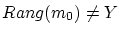 とすると,
とすると,
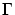 の定義から
の定義から
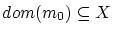 ,
,
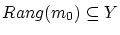 でしたから,
でしたから,
 であり,かつ
であり,かつ
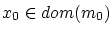 でない
でない
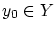 であり,かつ
であり,かつ
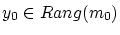 でない
でない
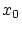 ,
,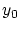 が存在することになります.
しかし,そうすると
が存在することになります.
しかし,そうすると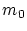 を拡張した
を拡張した
―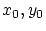 を夫々、
を夫々、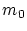 の定義域,値域に加え,
の定義域,値域に加え,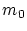 のグラフに
のグラフに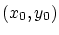 を追加して―
を追加して―
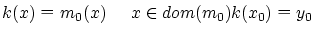 という双射が定義できますが…)
という双射が定義できますが…)
問題により
すなわち
です.
![$\left [{ 証明終り} \right]$](img163.png)



: 基数の集合の整列性
: 集合の基数
: 基数の順序関係
目次
Yasunari SHIDAMA
![]() の要素が尽きればそのとき
の要素が尽きればそのとき![]() から
から![]() への単射が作られていることになり
への単射が作られていることになり
![]() で逆に,
で逆に,![]() の要素が尽きれば
の要素が尽きれば
![]() です.
です.
![]() の要素が
の要素が
![]() や
や
![]() と番号付けできることを前提にしていますが(数学的帰納法を使うには添え字は自然数でなければならない)、例えば実数の集合の元にはそのような番号付けは出来ません.
と番号付けできることを前提にしていますが(数学的帰納法を使うには添え字は自然数でなければならない)、例えば実数の集合の元にはそのような番号付けは出来ません.![]()
![]() の部分集合で,値域が
の部分集合で,値域が![]() の部分集合である双射全体の集合
の部分集合である双射全体の集合![]() を考え,その
を考え,その![]() の任意の元
の任意の元
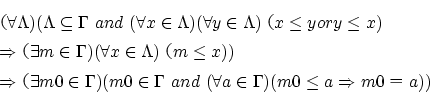
![]() の間には
の間には![]() から
から![]() へか,あるいは
へか,あるいは![]() から
から![]() への双射が存在することをを証明します.
への双射が存在することをを証明します.
![]() の部分集合で,値域が
の部分集合で,値域が![]() の部分集合である双射全体の集合
の部分集合である双射全体の集合
![]() の任意の元
の任意の元
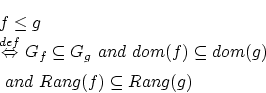
![]() が
が![]() 上の順序関係を定義していることを示して下さい.
上の順序関係を定義していることを示して下さい.
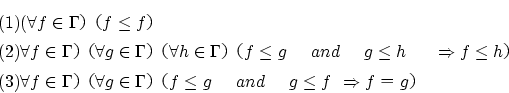
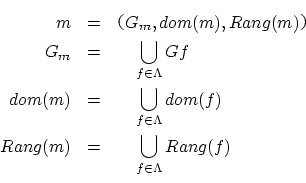
![]()