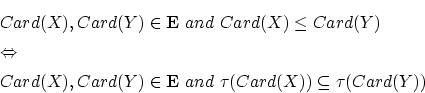


: この文書について...
: 集合の基数
: 基数の比較可能定理(Bernsteinの定理)
目次
最後に以下の定理を紹介し終わりとします。
[定理]
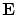 を基数の集合とするとき,
を基数の集合とするとき,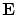 は順序
は順序
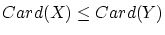 について整列順序集合である。
について整列順序集合である。
[証明]
集合族
を
の元から選びます。
とすると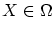 が存在して
が存在して
です。
とおくと,
整列可能性定理により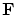 には整列順序
には整列順序
が定義される。
また,同定理の系によれば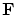 のべき集合
のべき集合
について,
は集合の包含関係の順序について整列集合であり,その任意の空でない部分集合は
最小元をもつので,写像
が定義される。
このとき,
実際,
から
同様に
よって,
逆に
とすると,
より,
が存在して
第4章の整列集合の同型定理の系3
によれば,
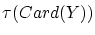 切片,
切片,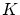 が存在して
が存在して
従って
よって
よって
後者の関係は整列順序であるから,
も整列順序
[証明終]

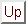


: この文書について...
: 集合の基数
: 基数の比較可能定理(Bernsteinの定理)
目次
Yasunari SHIDAMA
![]() を基数の集合とするとき,
を基数の集合とするとき,![]() は順序
は順序
![]() について整列順序集合である。
について整列順序集合である。
![]() には整列順序
には整列順序
![]() のべき集合
のべき集合
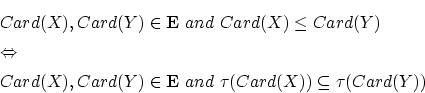
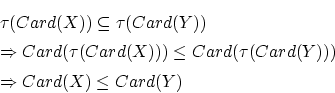
![]() 切片,
切片,![]() が存在して
が存在して