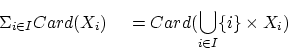


: 乗算
: 基数の演算
: 基数の演算
目次
基数
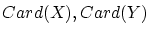 の加算を次のように定義できます。
の加算を次のように定義できます。
まず, 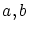 を
を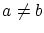 として
として
を作ります。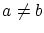 ゆえ
ゆえ
です。
と定義します。
これは
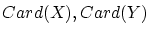 の代表元の取り方に依存しません。
[証明]
の代表元の取り方に依存しません。
[証明]
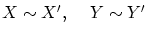 すなわち、
すなわち、
とすると、
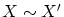 より 双射
より 双射
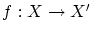 が存在します。
同様に
が存在します。
同様に
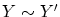 より 双射
より 双射
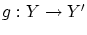 が存在します。
が存在します。
このとき写像
を定義すると、h、kは双射で
から
から
への双射j
が
で定義されます。
よって
すなわち
[証明終り]
問61(可換則, 結合則)
以下を証明してください。
特に
となります。
空集合 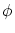 の基数
の基数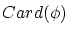 を
を 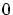 で表します。
で表します。
少し技巧的ですが
同様に
と定義します。
が成立っています。
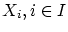 の基数の
の基数の
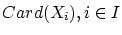 について
について
と定義します。



: 乗算
: 基数の演算
: 基数の演算
目次
Yasunari SHIDAMA
![]() を
を![]() として
として
![]() より 双射
より 双射
![]() が存在します。
同様に
が存在します。
同様に
![]() より 双射
より 双射
![]() が存在します。
が存在します。
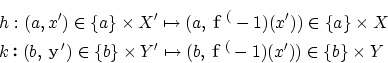
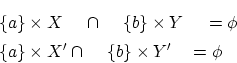
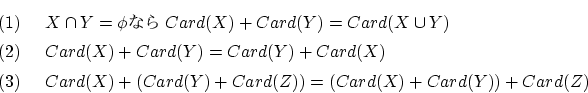
![]() の基数
の基数![]() を
を ![]() で表します。
で表します。
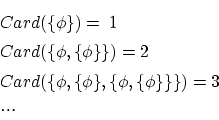
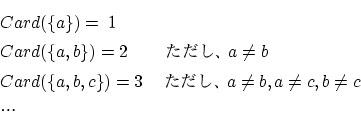
![]() の基数の
の基数の
![]() について
について