公理系

三角形$ABC$の内角の和が１８０°であることを示す平面幾何の証明を 思い出そう。これを示すには例えば，

1. 問題の三角形の底辺を$BC$として，それを右端点$C$から適当な長さだけ右へ 延長し端点を$D$としておく。
2. $C$を通り，斜辺$AB$に平行な補助線を引く。$A$の方向に延ばした端点をEとするので、これは$CE$となる。
3. 平行線と交差する直線と交わる角度についての性質から
   $$\begin{eqnarray*} &&∠CAB = ∠ACE \\ &&∠ABC = ∠ECD \\ &&∠ABC+∠BCA+∠CAB... ...E \\ &&∠ECD+∠BCA+∠ACE=180° \\ &&∠ABC+∠BCA+∠CAB=180° \end{eqnarray*}$$
   
   
   によって内角の和が１８０°であることを示す。

この証明を前節までの記号論理で表現すれば，

1. １点を通ってある直線に平行な直線が存在する。
   
   $$AB ／／ CE$$
   
   

2. ２本の平行線と交わる直線がつくる２つの同位角は等しい。
   
   $$AB ／／ CE \Rightarrow ∠ABC = ∠ECD$$
   
   

3. ２本の平行線と交わる直線がつくる２つの錯角は等しい。
   
   $$AB ／／ CE \Rightarrow ∠CAB = ∠ACE$$
   
   

4. 直線は１８０°である。
   
   $$∠ECD+∠BCA+∠ACE=180$$
   
   

5. $$\begin{eqnarray*} &&( ∠ABC = ∠ECD \land ∠CAB = ∠ACE) \\ &&\Rightarrow \\ &&(∠ABC+∠BCA+∠CAB=∠ECD+∠BCA+∠ACE) \end{eqnarray*}$$
   
   

6. 
   
   $$∠ABC+∠BCA+∠CAB=180$$
   
   

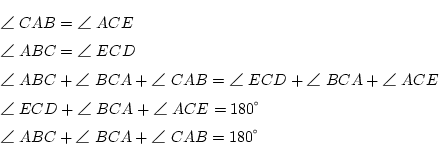
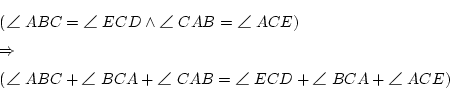
という表現であろう。

$1,2,3,4$のような公理と呼ばれる数少ない（自明とされる）論理式から 三角形$ABC$の内角の和が１８０°ということを表す$6$のような論理式 を三段論法と呼ばれる推理規則で導いている。
公理系と呼ばれる ${\bf L_g}$ の部分集合 ${\bf\alpha}$ と推論規則が適当に定めら れ，恒真論理式が ${\bf\alpha}$ から推論規則によって導けるような体系を, 命題論理の公理的体系という。
　　中学校時代に学んだ平面幾何学は ユーグリッド幾何学と呼ばれているが，それには有名な平行線の公理など， ユーグリッドが選んだいくつかの公理が用いられている。
　　ギリシャ時代発明された 論理学はこの幾何学の発達とともに発達したと言っても良いだろう。

以下にこの教材で扱う公理系を示す。 $\cal A,B,C$ は任意の ${\bf L_g}$ の要素，すなわち論理式とする。 ${\bf 公理系 \alpha}$ として，次の $(1) \sim (15)$ をとる。

(1).

$\cal A \Rightarrow A$

(2).

$\cal (A \Rightarrow B) \Rightarrow [(B \Rightarrow C) \Rightarrow (A \Rightarrow C)]$

(3).

$\cal (A \land B) \Rightarrow B$

(4).

$\cal (A \land B) \Rightarrow A$

(5).

$\cal (A \Rightarrow C) \Rightarrow \{ (B \Rightarrow C) \Rightarrow [(A \lor B) \Rightarrow C]\}$

(6).

$\cal B \Rightarrow (A \lor B)$

(7).

$\cal A \Rightarrow (A \lor B)$

(8).

$\cal (C \Rightarrow A) \Rightarrow \{ (C \Rightarrow B) \Rightarrow [C \Rightarrow (A \land B)]\}$

(9).

$\cal [A \land (A \Rightarrow B)] \Rightarrow B$

(10).

$[{\cal (A \land B)} \Rightarrow F ] \Rightarrow {\cal (B \Rightarrow \neg A)}$

(11).

${\cal (A \land \neg A)} \Rightarrow F$

(12).

$\cal [(A \land C) \Rightarrow B] \Rightarrow [C \Rightarrow (A \Rightarrow B)]$

(13).

${\cal A} \Rightarrow T$

(14).

$F \Rightarrow {\cal A}$

(15).

$\cal A \lor \neg A$