


: 演繹定理
: 命題論理の公理系
: 公理系
前節の公理から何らかの記号的な操作によって証明可能な論理式が得られるの
であるがその操作の規則を推論規則とよぶ。
命題論理での推論規則は,次の三段論法(modus ponens)のみである。
横線の上の論
理式から下の論理式が導かれることを表す。
証明可能性を定義する。すなわち,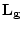 の要素である論理式のうち,
証明可能な論理式(provable formula)を次のように定める:
の要素である論理式のうち,
証明可能な論理式(provable formula)を次のように定める:
- (1).
- 公理系の各公理の形の論理式は証明可能である。
- (2).
- 論理式
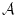 と論理式
と論理式
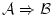 が証明可能なら
ば,(推論規則によって,)論理式
が証明可能なら
ば,(推論規則によって,)論理式 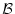 は証明可能である。
は証明可能である。
証明可能な論理式の列を「証明」という。「証明可能性」の定義に従えば
が「証明」のとき,各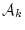 は
は
- (1).
- 公理系の各公理の形の論理式である。
- (2).
- 論理式
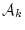 の前に論理式
の前に論理式 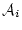 と
と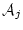
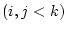 があり,
があり,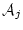 は
は
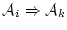 の
形をしている。
の
形をしている。
例えば,
もっと具体的には
は証明である。(証明可能な論理式を「定理」とか「命題」と呼ぶこともある。)
「証明」の中で推論規則と公理を何回か適用する共通した手順を「推論法則」
と呼ぶ。(これ自身は公理系を定義するのに必須ではないが,それを操作する
上で便利な手続きをまとめたもの。)
以下に推論法則の例を述べる。
[例]
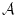 が証明可能な論理式ならば
が証明可能な論理式ならば
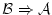 も
証明可能な論理式であることを表す。
も
証明可能な論理式であることを表す。
実際,上の「証明」の例の最後に注目すれば
は証明可能であり,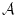 が証明可能なら推論規則(三段論法)
により,
が証明可能なら推論規則(三段論法)
により,
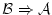 も証明可能なことがわかる。
も証明可能なことがわかる。
任意の論理式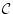 を用いて「添加」により
を用いて「添加」により
が証明可能である。また公理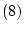 から
から
推論規則により,
が証明可能である。ところで公理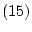 により
により
は公理(当然証明可能な論理式であるから)
結局,
は証明可能な論理式である。 またこれから直ちに
またこれから直ちに
が得られる。
同様に
も得られる。さらに
も得られる。
これは公理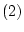 より
より
が証明可能であり,これと
から推論規則により,
証明可能である。さらにこれと
とから
が証明可能であることで示される。 同様に
同様に
が証明可能である。これはまず,公理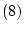 から
から
これと
から
が証明可能であり,
さらに公理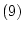 の
の
と前述の「推移」により
が証明可能であることで示される。
上述の体系を 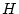 と呼ぶことにしよう。(
と呼ぶことにしよう。(
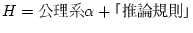 )
)
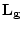 の論理式
の論理式 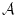 が証明可能であるとは,
が証明可能であるとは,
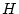 において,公理系
において,公理系 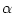 から
から 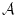 が推論規
則によって導けることであるから,これを
が推論規
則によって導けることであるから,これを
と書く。推論規則
はこの表記法を用いると,
と書くべきである。しかし,どの系で証明可能なのか明らかな場合は
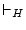 は省略することにする。
は省略することにする。



: 演繹定理
: 命題論理の公理系
: 公理系
Yasunari SHIDAMA
![]() と呼ぶことにしよう。(
と呼ぶことにしよう。(
![]() )
)
![]() の論理式
の論理式 ![]() が証明可能であるとは,
が証明可能であるとは,
![]() において,公理系
において,公理系 ![]() から
から ![]() が推論規
則によって導けることであるから,これを
が推論規
則によって導けることであるから,これを