![]() が成り立つとすると,
系
が成り立つとすると,
系![]() の「証明」である論理式の列
の「証明」である論理式の列
があって,
- (1).
- 公理系の各公理の形の論理式である。この場合,各公理は恒真論理式
であるから
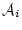 は恒真論理式である。
は恒真論理式である。
- (2).
- 論理式
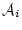 の前に論理式
の前に論理式 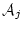 と
と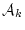
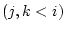 があり,
があり,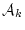 は
は
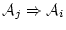 の
形をしている。
の
形をしている。
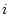 より前の論理式は恒真論理式であると仮定すると,
より前の論理式は恒真論理式であると仮定すると,
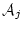 と
と
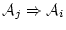 が真理値
が真理値 しかとらないから真理値表
しかとらないから真理値表
から明らかなように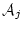
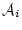
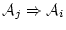
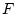
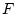

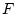



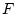
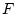



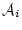 の真理値は
の真理値は しか取り得ない。
すなわち
しか取り得ない。
すなわち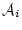 は恒真論理式である。
は恒真論理式である。
となるような論理式は存在しない。
![]() が命題変数
が命題変数
![]() から構成される論理式とする。
命題変数
から構成される論理式とする。
命題変数
![]() に真理値
に真理値![]() をふり当て,そのふり当てに対し
をふり当て,そのふり当てに対し![]() の真理値が
の真理値が![]() である場合
である場合
である。ただし,![]() は
は![]() に対する真理値のふり当てが
に対する真理値のふり当てが![]() の場合
の場合![]() ,
,![]() の場合は
の場合は![]() とする。
とする。![]()
恒真論理式![]() が命題変数
が命題変数
![]() から構成されるものとする。
命題変数
から構成されるものとする。
命題変数
![]() に真理値
に真理値![]() をどのようにふり当てても,
をどのようにふり当てても,
![]() の真理値は常に
の真理値は常に![]() である。
である。
命題変数
![]() に真理値
に真理値![]() どのようにふり当てるしかたは
どのようにふり当てるしかたは
![]() 通りある。これを辞書式順序で全て列挙し[補題]を適用すると
通りある。これを辞書式順序で全て列挙し[補題]を適用すると
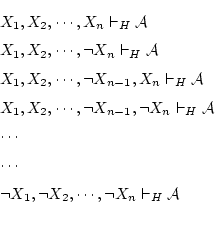
が得られる。最初の2式から演繹定理により
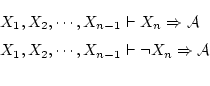
これから公理
が得られる。すなわち
を得る。
- 論理式
 がただ1つの命題変数
がただ1つの命題変数 からなるとき
からなるとき
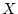 に対するふり当てが
に対するふり当てが のとき
のとき
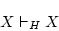
 のとき
のとき
これは公理の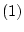 から容易に示される。
から容易に示される。
これ以外の場合は,
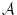 は
は
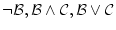 の形をして
いる。この場合,部分式
の形をして
いる。この場合,部分式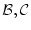 については
この補題が成り立つものとする。
については
この補題が成り立つものとする。
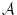 が
が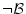 である場合
である場合
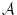 の値が
の値が のとき
のとき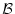 の値は
の値は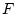 であるから
であるから
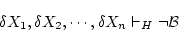
 の値が
の値が のとき
のとき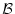 の値は
の値は であるから
であるから
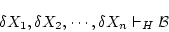
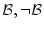 はそれぞれ
はそれぞれ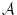 及び
及び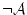 である。
である。
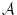 が
が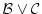 である場合
である場合
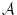 の値が
の値が のとき
のとき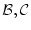 の少なくともどちらか一方の値は
の少なくともどちらか一方の値は
 であるから,
であるから,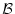 の値が
の値が としても一般性を失わない。このとき
としても一般性を失わない。このとき
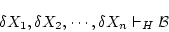
が成り立っている。これと公理の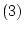
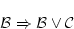
により
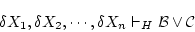
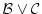 は
は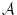 に他ならない。
に他ならない。
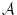 の値が
の値が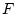 のとき
のとき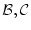 の値はともに
の値はともに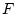 でなければならない。
このとき
でなければならない。
このとき
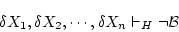
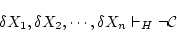
これに推論法則の「論理積」
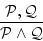
を用いて
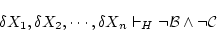
を得る。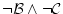 は
は
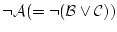 に他ならない。
に他ならない。
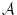 が
が
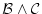 である場合
である場合
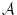 の値が
の値が のとき
のとき の値はともに
の値はともに でなければならない。
このとき
でなければならない。
このとき
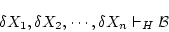
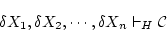
これに推論法則の「論理積」
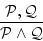
を用いて
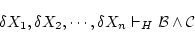
を得る。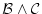 は
は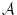 に他ならない。
に他ならない。
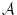 の値が
の値が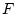 のとき
のとき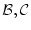 の少なくともどちらか一方の値は
の少なくともどちらか一方の値は
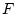 であるから,
であるから,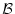 の値が
の値が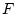 としても一般性を失わない。このとき
としても一般性を失わない。このとき
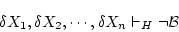
が成り立っている。これと公理の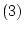
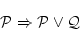
により
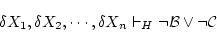
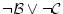 は
は
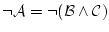 に他ならない。
に他ならない。