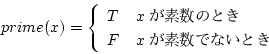: 述語の論理和・論理積・否定
: 述語論理
: 述語論理
命題論理では真理値の集合である
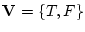 が定義されたが,述語論理ではさらに,
何らかの対象の集合
が定義されたが,述語論理ではさらに,
何らかの対象の集合 も定義される。これは具体的には
整数の集合
も定義される。これは具体的には
整数の集合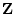 や実数の集合
や実数の集合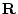 であったり,あるいは
日本人全体の集合といったものを表したりする。
であったり,あるいは
日本人全体の集合といったものを表したりする。 は空で
ないことが要求される。この
は空で
ないことが要求される。この から
から
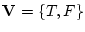 への写像
への写像
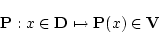 |
(3.1) |
を1変数の命題関数(propositional function)と呼ぶ。
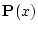 を1変数の述語(predicate)と呼ぶ。
を1変数の述語(predicate)と呼ぶ。
領域 が複数の集合の直積集合
が複数の集合の直積集合
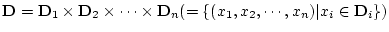 である場合も考えることできる。これを明示したいときは,
である場合も考えることできる。これを明示したいときは,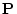 を
を 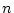 変数の命題関
数,その表現を
変数の命題関
数,その表現を 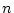 変数の述語という。
変数の述語という。
また,集合  を
を 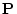 の対象領域(objectdomain)と呼び,
の対象領域(objectdomain)と呼び, の各
要素を
の各
要素を 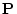 の対象という。
すなわち,
の対象という。
すなわち,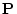 は対象領域
は対象領域  上で定義された命題関数であり,
上で定義された命題関数であり,
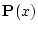 は
は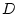 上の述語である。
上の述語である。
たとえば,自然数の全体 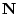 で定義される写像
で定義される写像
を
と定義すれば,この写像は 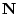 上の(1変数)命題関数であり,
上の(1変数)命題関数であり,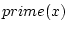 は
は 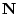 上の(1変数)述語である。
この述語は
上の(1変数)述語である。
この述語は
という主張を意味する。
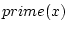 は,
は,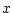 が素数のとき
が素数のとき 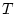 ,
素数でないとき
,
素数でないとき 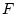 である。
一般に,命題関数
である。
一般に,命題関数
に対し,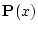 を「
を「
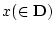 は
は 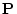 である」と読む。
である」と読む。
Yasunari SHIDAMA
![]() が複数の集合の直積集合
が複数の集合の直積集合
![]() である場合も考えることできる。これを明示したいときは,
である場合も考えることできる。これを明示したいときは,![]() を
を ![]() 変数の命題関
数,その表現を
変数の命題関
数,その表現を ![]() 変数の述語という。
変数の述語という。
![]() を
を ![]() の対象領域(objectdomain)と呼び,
の対象領域(objectdomain)と呼び,![]() の各
要素を
の各
要素を ![]() の対象という。
すなわち,
の対象という。
すなわち,![]() は対象領域
は対象領域 ![]() 上で定義された命題関数であり,
上で定義された命題関数であり,
![]() は
は![]() 上の述語である。
上の述語である。
![]() で定義される写像
で定義される写像