


: 項述語
: 述語論理
: 述語論理
命題論理では,命題を真偽だけをもつ変数として,内容には立ち入らなかった。
などは総て,真(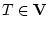 )として同一のものとして扱った。
これに対し,述語論理(
)として同一のものとして扱った。
これに対し,述語論理(
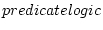 )では命題の内部構造も考察の対象になる。
)では命題の内部構造も考察の対象になる。
ここで再び,第一章で述べた三段論法
について考える。
命題論理では命題である
というソクラテスについての主張を
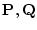 で表し,
で表し,
という記号列が得られるとしてその記号列の操作により正しい結論を得る方法を
調べた。
上のソクラテスに関する命題について「ソクラテス」の固有名詞の代わりに不特定
な対象を表す文字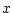 を用いた
を用いた
に換えてみよう。そしてこれらをそれぞれ
で表す。
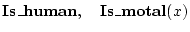 はそのままでは真理値が決まらない。
はそのままでは真理値が決まらない。
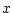 に具体的な
に具体的な や
や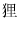 を代入して初めて定まる。即ち,前章までに定義した
命題になる。
を代入して初めて定まる。即ち,前章までに定義した
命題になる。
は何れも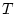 (真)であるが,
(真)であるが,
は前者は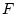 (偽)であり,後者は
(偽)であり,後者は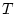 (真)となる。
(真)となる。
同様に
の真理値はそのままでは確定できない。しかし,
という主張は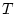 (真)である。
(真)である。
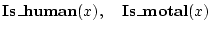 のように
のように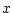 に特定の対象を代入したときに真偽が確定するものを述語という。
述語論理学では前章までの命題だけではなくこのような述語を含めた
正しい推論の方法を考察する。
に特定の対象を代入したときに真偽が確定するものを述語という。
述語論理学では前章までの命題だけではなくこのような述語を含めた
正しい推論の方法を考察する。
Yasunari SHIDAMA




![]() を用いた
を用いた
