


: 述語の公理系
: 述語論理
: 基本的な性質
ド・モルガンなどを用いれば,限定記号
 が
他の論理記号より,左側にあるように変形できる。これを冠頭標準形
が
他の論理記号より,左側にあるように変形できる。これを冠頭標準形
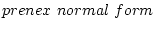 という。この節では冠頭標準形の導出法について述べる。
という。この節では冠頭標準形の導出法について述べる。
ここで簡単のため を有限集合
を有限集合
としておく。以下の結果は が無限集合でも成り立つ。
が無限集合でも成り立つ。
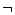 の右側への移動
の右側への移動
定理8.1
定義と定理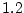 のド・モルガン則によれば,
のド・モルガン則によれば,
を得る。
- 限定記号
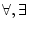 の左側への移動
の左側への移動
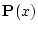 と
と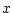 を含まない
を含まない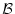 について
定義と定理
について
定義と定理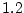 によれば,定理
によれば,定理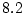 が成り立つ。
が成り立つ。
定理8.2
- 冠頭標準形の導出法
定理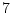 と
と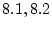 により以下の手順で冠頭標準形を導出することができる。
により以下の手順で冠頭標準形を導出することができる。
- 同じ変数名で自由変数と束縛変数が混在する場合は変数名を変更する。
例えば
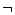 の右側への移動
の右側への移動
定理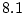 (ド・モルガン則)により
(ド・モルガン則)により
の形の変形を行う。
- 限定記号
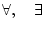 の左側への移動
の左側への移動
定理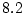 により
により
の形の変形を繰り返し行う。
さらに以上の手順と主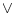 標準形(主
標準形(主 標準形)への変換アルゴリズム
を併用することもできる。
標準形)への変換アルゴリズム
を併用することもできる。



: 述語の公理系
: 述語論理
: 基本的な性質
Yasunari SHIDAMA
![]() を有限集合
を有限集合
![]() のド・モルガン則によれば,
のド・モルガン則によれば,