


: 公理
: 述語論理の公理系
: 述語論理の記号
命題論理と同様に論理式が以下のように再帰的に定義される。
限定記号で束縛されていない対象変数記号を自由変数記号という。
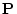 が
が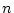 変数述語記号で
変数述語記号で
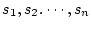 が項なら
が項なら
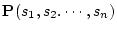 は論理式
は論理式
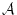 が論理式ならば、
が論理式ならば、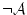 は論理式である。
は論理式である。
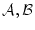 が論理式ならば、
が論理式ならば、
は、いずれも論理式である。
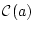 が対象変数記号
が対象変数記号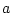 を含む論理式で,
を含む論理式で,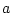 が自由変数記号のとき,
が自由変数記号のとき,
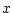 が
が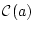 の中に現れない対象変数記号ならば
の中に現れない対象変数記号ならば
は、いずれも論理式である。
上の定義では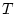 と
と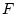 以外具体的な論理式は出てこない。
以外具体的な論理式は出てこない。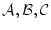 は不特定な論理式を表すメタ記号であって,具体的な論理式ではない。
しかし,命題論理の論理式と同様にこれらの規則で無数の論理式を作り
だすことができる。
は不特定な論理式を表すメタ記号であって,具体的な論理式ではない。
しかし,命題論理の論理式と同様にこれらの規則で無数の論理式を作り
だすことができる。
Yasunari SHIDAMA