


: 述語論理の記号
: 述語の公理系
: 述語の公理系
命題論理では真理値の集合
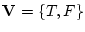 上での命題変数による論理演算を扱うだけであったので記号の表現が簡潔であったが,述語論理は対象領域
上での命題変数による論理演算を扱うだけであったので記号の表現が簡潔であったが,述語論理は対象領域 上の述語をも扱うためその分複雑になる。
上の述語をも扱うためその分複雑になる。
 はそれぞれの数学的理論が固定されて決まる。例えば,整数論なら
はそれぞれの数学的理論が固定されて決まる。例えば,整数論なら
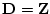 であるし,複素数の性質を扱う理論なら
であるし,複素数の性質を扱う理論なら
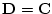 である。さらに述語は
である。さらに述語は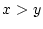 といった
といった の要素について単純な関係だけではなく,
の要素について単純な関係だけではなく,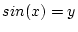 ,
,
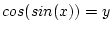 などのように
などのように の要素に
の要素に の上で定義される関数を作用させた,対象についての記述も含む。
の上で定義される関数を作用させた,対象についての記述も含む。
このため先ず の上の「項」という概念が必要になる。
項には以下の記号が用いられる。
の上の「項」という概念が必要になる。
項には以下の記号が用いられる。
- 対象定数記号
特定の対象を表す記号。
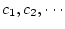 または
または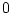 変数の関数
を表す
変数の関数
を表す
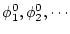 などを用いる。
などを用いる。
- 対象変数記号
 上の変数を表す記号。
上の変数を表す記号。
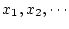 などを用いる。
などを用いる。
- 関数記号
 から
から への関数を表す記号。
への関数を表す記号。
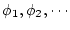 などを用いる。
などを用いる。
これらの記号を用いて項は「再帰的」に定義される。
- 対象定数記号は項である。
- 対象変数記号は項である。
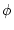 が
が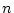 変数関数記号で
変数関数記号で
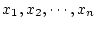 が項ならば,
が項ならば,
は項である。
Yasunari SHIDAMA