| (4.69) |
![]() この定理は,述語論理の体系についての妥当性と呼ばれるものである。
この定理は,述語論理の体系についての妥当性と呼ばれるものである。
![]() が成り立つとすると;
系
が成り立つとすると;
系![]() の「証明」である論理式の列
の「証明」である論理式の列
があって,
各![]() は
は
- (1).
- 公理系の各公理の形の論理式である場合、
公理
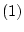 から
から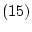 までは命題論理の公理系のそれと同じ形式で
容易に恒真論理式であることを示すことができる。
ここでは,
までは命題論理の公理系のそれと同じ形式で
容易に恒真論理式であることを示すことができる。
ここでは,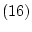 ,
,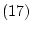 が恒真論理式であることを示そう。
任意の解釈
が恒真論理式であることを示そう。
任意の解釈
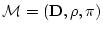 と対象変数記号と
と対象変数記号と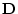 の要素との対応
の要素との対応
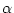 に対して,
に対して,
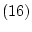 式については:
式については:
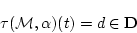
(4.70)
![$\displaystyle \tau({\cal M},{\bf\alpha})[(\forall x)({\cal C}(x)) \Rightarrow C(t)]$](img785.png)
![$\displaystyle =\tau({\cal M},{\bf\alpha})[\lnot (\forall x)({\cal C}(x))
\lor C(t)]$](img786.png)
![$\displaystyle =\lnot \tau({\cal M},{\bf\alpha})[(\forall x)({\cal C}(x))]
\lor \tau({\cal M},{\bf\alpha})[C(t)]$](img787.png)

\lor (\tau({\cal M},{\bf\alpha})[C](d)$](img788.png)

(4.71)
さらに右辺は
 \}
\lor \tau({\cal M},{\bf\alpha})[C](d)$](img789.png)
 \}$](img790.png)
![$\displaystyle \lor \lnot \tau({\cal M},{\bf\alpha})[{\cal C}(d)]
\lor \tau({\cal M},{\bf\alpha})[C](d)$](img791.png)
(4.72)
さらに続ければ
 \} \lor T$](img792.png)
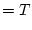
(4.73)
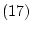 式については:
式については:
![$\displaystyle \tau({\cal M},{\bf\alpha})[{\cal C}(t)] \Rightarrow
(\exists x)({\cal C}(x))]$](img793.png)

\lor \tau({\cal M},{\bf\alpha})[(\exists x)({\cal C}(x) ) ]$](img794.png)

(4.74)
さらに右辺は

\lor \bigvee_{b \in {\bf D}}\tau({\cal M},{\bf\alpha})[{\cal C}](b)$](img795.png)

\lor \tau({\cal M},{\bf\alpha})[{\cal C}](d)$](img796.png)
$](img797.png)
$](img798.png)
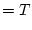
(4.75)
- (2).
- 論理式
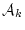 の前に論理式
の前に論理式 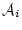 と
と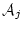
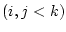 があり,
があり,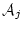 は
は
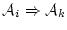 の
形をしている。
の
形をしている。
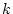 より前の論理式は恒真論理式であると仮定されているから,
より前の論理式は恒真論理式であると仮定されているから,
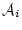 と
と
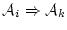 が真理値
が真理値 しかとらないから真理値表
しかとらないから真理値表
から明らかなように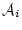
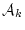
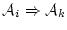




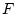



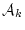 の真理値は
の真理値は しか取り得ない。
すなわち
しか取り得ない。
すなわち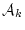 は恒真論理式である。
は恒真論理式である。
- (3).
- 論理式
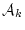 の前に論理式
の前に論理式 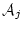
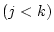 があり,
があり,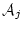 は
は
であり,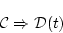
(4.76) 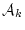 は
は
の形をしている場合。 ただし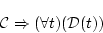
(4.77) 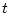 は自由変数記号で
は自由変数記号で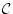 には現れないものとする。
この場合,まず,
には現れないものとする。
この場合,まず,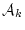 の
の
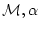 での真理値は
での真理値は
![$\displaystyle \tau({\cal M},{\bf\alpha})[{\cal C} \Rightarrow
(\forall t)({\cal D}(t))]$](img803.png)
![$\displaystyle =\lnot \tau({\cal M},{\bf\alpha})[{\cal C}] \lor
\bigwedge_{b \in {\bf D}} \tau({\cal M},{\bf\alpha})[{\cal C}](b)$](img804.png)
![$\displaystyle =\bigwedge_{b \in {\bf D}} \{
\lnot \tau({\cal M},{\bf\alpha})[{\cal C}] \lor
\tau({\cal M},{\bf\alpha})[{\cal C}](b) \}$](img805.png)
(4.78)
である。 しかし,帰納法の仮定から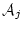 すなわち
すなわち
は 任意の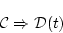
(4.79) 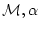 について
について
ゆえ任意の![\begin{displaymath}
\tau({\cal M},{\bf\alpha})[({\cal C} \Rightarrow {\cal D}(t)]=T
\end{displaymath}](img806.png)
(4.80) 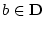 について
について
従って![\begin{displaymath}
\tau({\cal M},{\bf\alpha})[(\lnot {\cal C} \lor {\cal D}(b)]=T
\end{displaymath}](img807.png)
(4.81)
すなわち,![\begin{displaymath}
\bigwedge_{b \in {\bf D}} \{
\lnot \tau({\cal M},{\bf\alp...
...cal C}] \lor
\tau({\cal M},{\bf\alpha})[{\cal C}](b) \} =T
\end{displaymath}](img808.png)
(4.82)
最後に,![\begin{displaymath}
\tau({\cal M},{\bf\alpha})[{\cal C} \Rightarrow
(\forall t)({\cal D}(t))] =T
\end{displaymath}](img809.png)
(4.83) - (4).
- 論理式
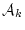 の前に論理式
の前に論理式 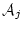
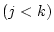 があり,
があり,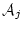 は
は
であり,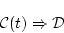
(4.84) 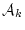 は
は
の形をしている場合を考えよう。 ただし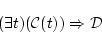
(4.85) 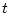 は自由変数記号で
は自由変数記号で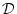 には現れないものとする。
まず,
には現れないものとする。
まず,
![$\displaystyle \tau({\cal M},{\bf\alpha})[
(\exists t)({\cal C}(t)) \Rightarrow {\cal D}]$](img812.png)

\lor {\cal D}$](img813.png)

\lor {\cal D}$](img814.png)
(4.86)
さらに右辺は

\lor {\cal D} \}$](img815.png)

\Rightarrow {\cal D} \}$](img816.png)
(4.87)
しかし帰納法の仮定から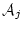 すなわち
すなわち
任意の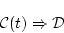
(4.88) 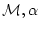 について
について
従って任意の![\begin{displaymath}
\tau({\cal M},{\bf\alpha})[{\cal C}(t) \Rightarrow {\cal D}]=T
\end{displaymath}](img817.png)
(4.89) 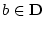 について
について
よって![\begin{displaymath}
\tau({\cal M},{\bf\alpha})[{\cal C}(b) \Rightarrow {\cal D}]=T
\end{displaymath}](img818.png)
(4.90)
すなわち
\Rightarrow {\cal D} \}=T
\end{displaymath}](img819.png)
(4.91)
![\begin{displaymath}
\tau({\cal M},{\bf\alpha})[
(\exists t)({\cal C}(t)) \Rightarrow {\cal D}] =T
\end{displaymath}](img820.png)
(4.92) 
| (4.93) |
この定理は,述語論理の体系についての無矛盾性と呼ばれるものである。
この定理は,述語論理の体系についての完全性定理(completeness theorem)と呼ばれるものである。
| (4.94) |
逆に![]() が恒真論理式であるときに,
が恒真論理式であるときに,
![]() が成立することをいうには次のHenkinの定理を
利用する。
が成立することをいうには次のHenkinの定理を
利用する。
| (4.95) |
任意の解釈![]() について
について
| (4.96) |
| (4.97) |
Henkinの定理の対偶によれば,
体系
![]() は矛盾する。
は矛盾する。
定理5によれば,任意の論理式![]() について
について
| (4.98) |
| (4.99) |
これらから 演繹定理8によれば
| (4.100) |
| (4.101) |
| (4.102) |
| (4.103) |
ここで,公理![]() によれば
によれば
| (4.104) |
| (4.105) |
- 定義
論理式の集合 に論理式
に論理式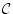 を加えた
を加えた
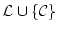 が矛盾するとき,
が矛盾するとき,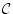 は
は と矛盾するという。
と矛盾するという。
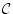 が
が と矛盾するときは必ず,
と矛盾するときは必ず, の有限部分集合
の有限部分集合
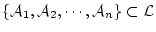 と矛盾している。
と矛盾している。
実際,
となる論理式
(4.106) 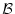 あれば,
あれば,
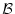 ,
,
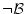 の証明である論理式の有限列
の証明である論理式の有限列
と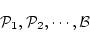
(4.107)
が存在するが,これらに現われる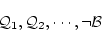
(4.108)  の論理式と公理は
有限個しかない。他の論理式は推論規則によって,上の有限列中に現われる
の論理式と公理は
有限個しかない。他の論理式は推論規則によって,上の有限列中に現われる
 の論理式と公理から導出されている。
従って,
の論理式と公理から導出されている。
従って,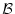 ,
,
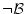 は有限個のLの論理式と公理
から導出される。
は有限個のLの論理式と公理
から導出される。
- 定義
論理式の集合 が無矛盾で,
が無矛盾で, に属さない総ての論理式が
に属さない総ての論理式が と矛盾するとき
と矛盾するとき を最大無矛盾集合という。
を最大無矛盾集合という。
- 定義
自由変数記号(限定記号で束縛されていない対象変数記号) を持たない論理式を個体閉論理式という。
- 補題
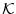 を述語論理の系
を述語論理の系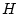 の個体閉論理式全体の集合とする。
の個体閉論理式全体の集合とする。
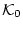 を
を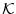 の無矛盾な部分集合とする。
の無矛盾な部分集合とする。
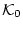 をその部分集合として含む最大無矛盾集合
をその部分集合として含む最大無矛盾集合
 が存在する。
が存在する。
- [補題の証明]
述語論理の論理式は対象定数記号,対象変数記号,論理記号,関数記号,述語記号を有限個並べた記号列であり,その論理式全体の集合は高々加算無限集合である。
(要素は無限個でもその要素一つ一つに自然数による番号を付与することができる。)
従って,論理式全体の集合の部分集合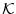 も高々加算である。
も高々加算である。
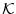 の要素である論理式に番号を付けておく。
の要素である論理式に番号を付けておく。
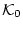 から初めて,以下の手順で,論理式の集合
から初めて,以下の手順で,論理式の集合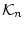 を構成する。
を構成する。
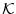 の
の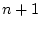 番目の論理式が
番目の論理式が
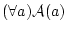 の形であるとき。
の形であるとき。
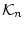 の論理式すべてと,
の論理式すべてと,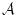 の中に現われない対象定数記号
の中に現われない対象定数記号
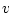 を選び,論理式
を選び,論理式
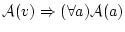 を
を
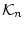 に追加して,
に追加して,
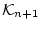 とする。即ち,
とする。即ち,
とする。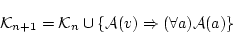
(4.109)  の
の 番目の論理式が
番目の論理式が
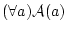 の形でないときは
何も追加せず
の形でないときは
何も追加せず
とする。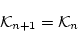
(4.110)
が得られるが,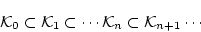
(4.111) 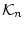 はすべて無矛盾集合である。
はすべて無矛盾集合である。
これを示すには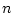 についての帰納法による。
についての帰納法による。
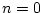 については
については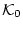 の仮定により,無矛盾。
の仮定により,無矛盾。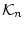 が無矛盾として
が無矛盾として
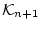 が矛盾するとすれば,ある論理式
が矛盾するとすれば,ある論理式 が存在して,
が存在して,
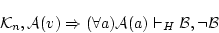
(4.112) 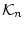 の論理式すべてと,
の論理式すべてと,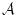 の中に現われない対象変数記号
の中に現われない対象変数記号
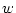 を選べば,
を選べば,
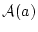 の
の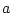 を
を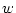 に書き換えた論理式を
に書き換えた論理式を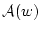 とすると
とすると
から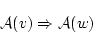
(4.113)
よって,![\begin{displaymath}[{\cal A}(w) \Rightarrow (\forall a) {\cal A}(a)]
\Rightarrow
[{\cal A}(v) \Rightarrow (\forall a) {\cal A}(a)]
\end{displaymath}](img859.png)
(4.114)
こから演繹定理により,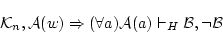
(4.115)
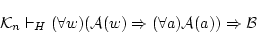
(4.116)
これらから,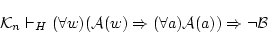
(4.117)
を得て,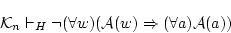
(4.118) 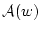 では
では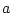 は自由変数でないから冠頭標準形の議論により,
は自由変数でないから冠頭標準形の議論により,
従って,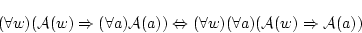
(4.119)
これから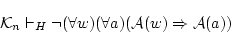
(4.120)
しかし,公理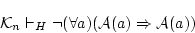
(4.121) 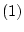 と推論規則「全称化」によれば,
と推論規則「全称化」によれば,
従って,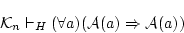
(4.122)  は矛盾する。これは帰納法の仮定に反する。
よって
は矛盾する。これは帰納法の仮定に反する。
よって
 は無矛盾。
は無矛盾。
結局,無矛盾な個体閉論理式の集合の増大列
が得られていた。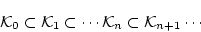
(4.123)
ここで,
とおけば,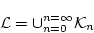
(4.124)  も無矛盾である。
実際,
も無矛盾である。
実際,
となる論理式
(4.125)  あれば,
あれば,
 ,
,
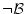 の証明である論理式の有限列
の証明である論理式の有限列
と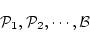
(4.126)
が存在するが,これらに現われる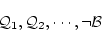
(4.127)  の論理式と公理は
有限個しかない。他の論理式は推論規則によって,上の有限列中に現われる
の論理式と公理は
有限個しかない。他の論理式は推論規則によって,上の有限列中に現われる
 の論理式と公理から導出されている。
従って,
の論理式と公理から導出されている。
従って,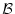 ,
,
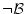 は有限個の
は有限個の の論理式と公理
から導出される。
の論理式と公理
から導出される。
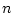 を十分大きく取れば,
を十分大きく取れば,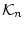 がそれらの論理式を全てその要素と
してもち,これは
がそれらの論理式を全てその要素と
してもち,これは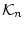 自身が既に矛盾することを示す。
自身が既に矛盾することを示す。

- 最大無矛盾集合
 は以下の性質をもつ。
は以下の性質をもつ。
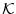 に属する論理式
に属する論理式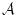 が
が の元なら
の元なら
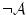 は
は の元でない
の元でない
実際,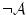 も
も の元なら
の元なら は矛盾する。
は矛盾する。
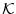 の論理式
の論理式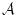 が
が の元でないならば
の元でないならば
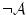 は
は の元である。
の元である。
実際,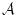 が
が の元でないなら
の元でないなら の最大性により,
の最大性により,
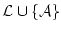 は矛盾。従って論理式
は矛盾。従って論理式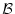 が存在して
が存在して
これらから 演繹定理8によれば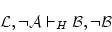
(4.128)
対偶をとれば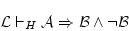
(4.129)
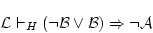
(4.130) ここで,公理
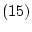 によれば
によれば
従って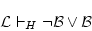
(4.131)
を得る。従って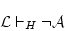
(4.132) 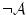 は
は と無矛盾。従って
これの元となる。
と無矛盾。従って
これの元となる。
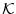 に属する論理式
に属する論理式
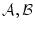 が両方とも
が両方とも の元であるとき,
の元であるとき,
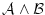 は
は の元である。
の元である。
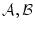 が両方とも
が両方とも の元なら推論規則「論理積」により
の元なら推論規則「論理積」により
で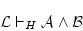
(4.133) 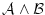 は
は と無矛盾。
と無矛盾。
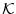 に属する論理式
に属する論理式
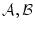 のどちらか一方が
のどちらか一方が の
元でないとき,
の
元でないとき,
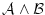 は
は の元でない。
の元でない。
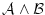 が
が の元なら,
公理
の元なら,
公理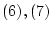 から
から
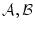 の何れも
の何れも と矛盾しない。
これから
と矛盾しない。
これから
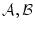 の何れも
の何れも の元なる。
の元なる。
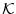 に属する論理式
に属する論理式
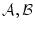 がのどちらか一方が
がのどちらか一方が の元であるとき,
の元であるとき,
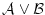 は
は の元である。
の元である。
証明は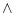 の場合と双対であるから省略する。
の場合と双対であるから省略する。
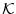 に属する論理式
に属する論理式
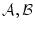 が両方とも
が両方とも の元でないとき,
の元でないとき,
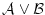 は
は の元でない。
の元でない。
証明は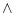 の場合と双対であるから省略する。
の場合と双対であるから省略する。
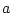 を対象変数記号,
を対象変数記号,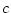 を対象定数記号とする。
すべての
を対象定数記号とする。
すべての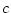 について
について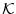 に属する論理式
に属する論理式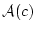 が
が の元であるとき,
の元であるとき,
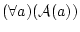 は
は の元である。
の元である。
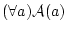 が
が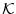 の
の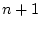 番目の個体閉論理式とすると,
番目の個体閉論理式とすると,
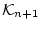 の構成法から
の構成法から
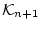 は,
論理式
は,
論理式
を元にもつ。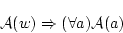
(4.134) 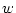 は
は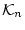 の全ての論理式と
の全ての論理式と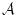 に現われない対象変数記号である。仮定から,
に現われない対象変数記号である。仮定から,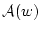 は
は の元ゆえ,
の元ゆえ,
も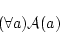
(4.135)  と矛盾せず,
と矛盾せず, の最大性から
の最大性から
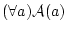 は,
は, の元となる。
の元となる。
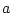 を対象変数記号,
を対象変数記号,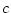 を対象定数記号とする。
少なくとも一つの
を対象定数記号とする。
少なくとも一つの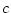 について
について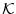 に属する論理式
に属する論理式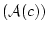 が
が の元でないとき,
の元でないとき,
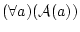 は
は の元でない。
の元でない。
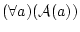 は
は の元ならば,公理
の元ならば,公理
 により,
により,
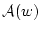 について
について
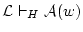 であり,従って,
であり,従って, と矛盾しない
から,その元になる。
と矛盾しない
から,その元になる。
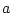 を対象変数記号,
を対象変数記号,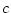 を対象定数記号とする。
少なくとも一つの
を対象定数記号とする。
少なくとも一つの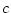 について
について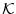 に属する論理式
に属する論理式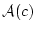 が
が の元であるとき,
の元であるとき,
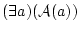 は
は の元である。
の元である。
証明は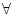 の場合と双対であるから省略する。
の場合と双対であるから省略する。
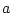 を対象変数記号,
を対象変数記号,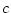 を対象定数記号とする。
すべての
を対象定数記号とする。
すべての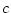 について
について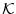 に属する論理式
に属する論理式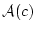 が
が の元で
ないならば,
の元で
ないならば,
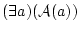 は
は の元でない。
の元でない。
証明は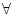 の場合と双対であるから省略する。
の場合と双対であるから省略する。
- 最大無矛盾集合
 を用いた
を用いた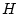 の解釈
の解釈
以下のように解釈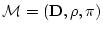 を構成する。
を構成する。
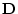 を対象定数記号全体の集合とする。
を対象定数記号全体の集合とする。
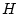 の対象変数記号に
の対象変数記号に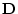 の要素
を対応させる対応
の要素
を対応させる対応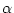 は任意にとる。
は任意にとる。
- 関数記号と
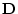 上の関数との対応
上の関数との対応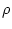 :
:
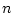 変数の関数記号の全体
変数の関数記号の全体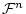 と
と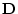 上の関数全体の集合
上の関数全体の集合
の間の対応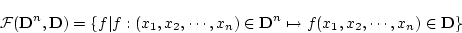
(4.136) 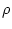 は
は
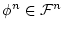 に対して
に対して
で定義する。(結局,恒等対応で,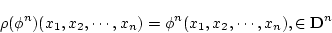
(4.137) 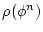 は
は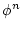 の定義域を
の定義域を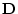 に制限するだけである。)
に制限するだけである。)
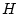 の述語記号と
の述語記号と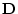 上の述語との対応 :
上の述語との対応 :
真理値の集合を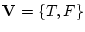 ,
,
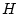 の
の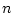 変数の述語記号の
全体の集合
変数の述語記号の
全体の集合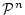 と,
と,
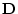 上の
上の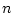 変数の述語全体の集合
変数の述語全体の集合
の間の対応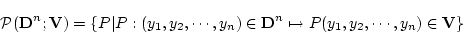
(4.138)
については,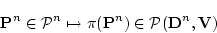
(4.139) 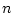 変数の述語記号
変数の述語記号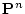 に
に
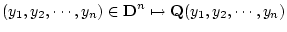
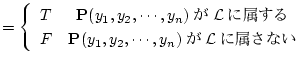
となる述語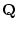 を対応させる。
を対応させる。
 の任意の論理式
の任意の論理式 について
について
 が
が の元でないとき
の元でないとき
![\begin{displaymath}
\tau({\cal M},{\alpha})[{\cal A}]=F
\end{displaymath}](img897.png)
(4.140) また
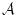 が
が の元のとき
の元のとき
![\begin{displaymath}
\tau({\cal M},{\alpha})[{\cal A}]=T
\end{displaymath}](img898.png)
(4.141) これは論理式
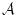 の記号列のとしての長さについての帰納法による。
の記号列のとしての長さについての帰納法による。
- 論理式
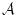 が
が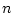 変数述語記号
変数述語記号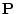 と項
と項
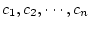 を用いて
を用いて
で表されるとき: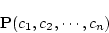
(4.142)
が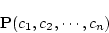
(4.143)  に属すれば
に属すれば
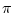 の定義から,
の定義から,
![\begin{displaymath}
\tau({\cal M},{\alpha})[{\cal A}]=\pi ({\bf P})(c_1,c_2,\cdots,c_n)=T
\end{displaymath}](img902.png)
(4.144)  に属さなければ
に属さなければ
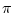 の定義から,
の定義から,
![\begin{displaymath}
\tau({\cal M},{\alpha})[{\cal A}]=\pi ({\bf P})(c_1,c_2,\cdots,c_n)=F
\end{displaymath}](img903.png)
(4.145) - 論理式
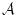 が
が
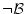 の形をしている場合。
の形をしている場合。
-
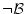 が
が に属すれば
に属すれば
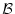 は
は に属さない。この論理式の長さは
に属さない。この論理式の長さは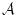 より短いので,帰納法の仮定により,
より短いので,帰納法の仮定により,
よって![\begin{displaymath}
\tau( {\cal M},{\bf\alpha})[{\cal B}]=F
\end{displaymath}](img904.png)
(4.146)
![\begin{displaymath}
\tau({\cal M},{\bf\alpha})[{\cal A}]
=\lnot \tau({\cal M},{\bf\alpha })[{\cal B}]=T
\end{displaymath}](img905.png)
(4.147) -
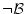 が
が に属さなければ
に属さなければ
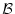 は
は に属す。この論理式の長さは
に属す。この論理式の長さは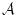 より短いので,帰納法の仮定により,
より短いので,帰納法の仮定により,
よって![\begin{displaymath}
\tau({\cal M},{\bf\alpha})[{\cal B}]=T
\end{displaymath}](img906.png)
(4.148)
![\begin{displaymath}
\tau({\cal M},{\bf\alpha})[{\cal A}]
=\lnot \tau({\cal M},{\bf\alpha})[{\cal B}]=F
\end{displaymath}](img907.png)
(4.149)
-
- 論理式
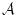 が
が
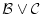 の形をしている場合。
の形をしている場合。
-
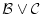 が
が に属せば
に属せば
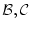 のうち少なくとも一方は
のうち少なくとも一方は に属する。
これらの論理式の長さは
に属する。
これらの論理式の長さは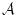 より短いので,帰納法の仮定により,
より短いので,帰納法の仮定により,
または![\begin{displaymath}
\tau({\cal M},{\bf\alpha})[{\cal B}]=T
\end{displaymath}](img906.png)
(4.150)
よって![\begin{displaymath}
\tau({\cal M},{\bf\alpha})[{\cal C}]=T
\end{displaymath}](img910.png)
(4.151)
![\begin{displaymath}
\tau({\cal M},{\bf\alpha})[{\cal A}]
=\tau({\cal M},{\bf...
...})[{\cal B}]
\lor \tau({\cal M},{\bf\alpha } )[{\cal C}]=T
\end{displaymath}](img911.png)
(4.152) -
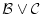 が
が に属さなければ
に属さなければ
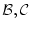 の何れも
の何れも に属さない。
に属さない。
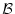 は
は に属す。この論理式の長さは
に属す。この論理式の長さは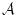 より短いので,帰納法の仮定により,
より短いので,帰納法の仮定により,
かつ![\begin{displaymath}
\tau( {\cal M},{\bf\alpha})[{\cal B}]=F
\end{displaymath}](img904.png)
(4.153)
よって![\begin{displaymath}
\tau({\cal M},{\bf\alpha})[{\cal C}]=F
\end{displaymath}](img912.png)
(4.154)
![\begin{displaymath}
\tau({\cal M},{\bf\alpha})[{\cal A}]=
\tau({\cal M},{\bf...
...ha})[{\cal B}]
\lor \tau({\cal M},{\bf\alpha})[{\cal C}]=F
\end{displaymath}](img913.png)
(4.155)
-
- 論理式
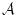 が
が
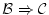 の形をしている場合。
の形をしている場合。
で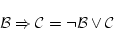
(4.156)  の結果を用いて示すことができるので省略する。
の結果を用いて示すことができるので省略する。
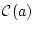 が対象変数記号
が対象変数記号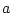 を含む論理式で,
を含む論理式で,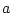 が自由変数記号,
が自由変数記号,
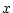 を
を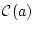 の中に現れない対象変数記号,
の中に現れない対象変数記号,
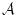 が
が
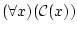 の形をしているとき。
の形をしているとき。
-
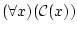 が
が に属すれば
に属すれば
 の性質について述べたことから,
すべての対象定数記号
の性質について述べたことから,
すべての対象定数記号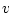 について
について
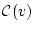 は
は の元。従って,
の元。従って,
ここで,![\begin{displaymath}
\tau({\cal M},{\bf\alpha})[{\cal C}(v)]=
\tau({\cal M},{\bf\alpha})[{\cal C}](v)=T
\end{displaymath}](img919.png)
(4.157) 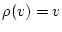 に注意する。
従って,
に注意する。
従って,
![\begin{displaymath}
\tau({\cal M},{\bf\alpha})[(\forall x)({\bf\cal C}(x))]
=...
...edge_{b \in {\bf D}}\tau({\cal M},{\bf\alpha})[{\cal C}](b)=T
\end{displaymath}](img921.png)
(4.158) -
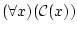 が
が に属さなければ
に属さなければ
 の性質について述べたことから,
ある対象定数記号
の性質について述べたことから,
ある対象定数記号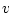 について
について
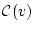 は
は の元でない。従って,
の元でない。従って,
従って,![\begin{displaymath}
\tau({\cal M},{\bf\alpha})[{\cal C}(v)]=
\tau({\cal M},{\bf\alpha})[{\cal C}](v)=F
\end{displaymath}](img922.png)
(4.159)
![\begin{displaymath}
\tau({\cal M},{\bf\alpha})[(\forall x)({\cal C}(x))]
=\bigwedge_{b \in {\bf D}}\tau({\cal M},{\bf\alpha})[{\cal C}](b)=F
\end{displaymath}](img923.png)
(4.160)
-
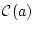 が対象変数記号
が対象変数記号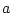 を含む論理式で,
を含む論理式で,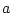 が自由変数記号,
が自由変数記号,
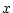 を
を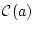 の中に現れない対象変数記号,
の中に現れない対象変数記号,
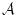 が
が
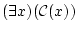 の形をしているとき。
これも
の形をしているとき。
これも
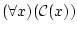 の場合と双対的にできるので省略する。
の場合と双対的にできるので省略する。
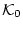 は
は の部分集合である。
の部分集合である。
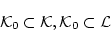
(4.161) 従って,
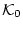 の任意の論理式
の任意の論理式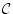 について
について
即ち,![\begin{displaymath}
\tau({\cal M},{\bf\alpha})[{\cal C}]=T
\end{displaymath}](img926.png)
(4.162) 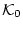 は充足可能である。
は充足可能である。
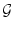 から無矛盾な個体閉論理式の集合
から無矛盾な個体閉論理式の集合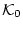 を作る。
を作る。
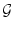 の論理式の自由変数記号に対象定数記号を
代入する。こうしてできる論理式は個体閉論理式である。
の論理式の自由変数記号に対象定数記号を
代入する。こうしてできる論理式は個体閉論理式である。
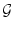 の総ての論理式のこの操作を施して作った
論理式の集合を
の総ての論理式のこの操作を施して作った
論理式の集合を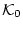 で表す。
で表す。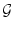 が無矛盾
ゆえ
が無矛盾
ゆえ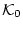 は無矛盾である。
は無矛盾である。
例
から自由変数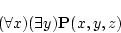
(4.163) 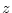 に対象定数記号
に対象定数記号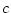 を代入すると
を代入すると
を得る。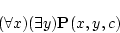
(4.164) - 個体閉論理式の集合
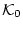 が無矛盾であれば,充足可能な
ことは示した。さらに
が無矛盾であれば,充足可能な
ことは示した。さらに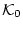 の
の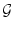 からの構成法から
からの構成法から
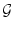 は充足可能である。
は充足可能である。