導出原理

ここで恒真論理式

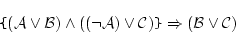$$\verb\vert{\vert{({\cal A } \lor {\cal B}) \land ((\lnot {\... ...l C})\verb\vert}\vert} \Rightarrow ({\cal B } \lor {\cal C})$$ (5.24)

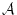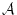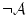に注目しよう。これは${\cal A}$のリテラル(${\cal A}$または $\lnot {\cal A}$) を共通にもつ２つの節から共通のリテラルが消去された１つの節を導くものと 解釈できる。
節の数が減り，形がより単純化されることに注意しておく。 これを推論規則として

$$\frac{{\cal A } \lor {\cal B} ,\lnot {\cal A } \lor {\cal C}} {{\cal B } \lor {\cal C}}$$

と表し，導出原理と呼ぶ。

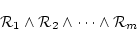$${\cal R}_1 \land {\cal R}_2 \land \cdots \land {\cal R}_m$$ (5.25)

に上の推論規則「導出原理」を繰り返し適用して，節の数が，最後に

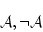$${\cal A } ,\lnot {\cal A }$$ (5.26)

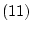
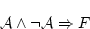の２つだけになったとすると，これと公理$(11)$

$${\cal A } \land \lnot {\cal A } \Rightarrow F$$ (5.27)

から矛盾が導き出されたことになる。これを「空節」の 導出として

$$\frac{{\cal A } ,\lnot {\cal A } } { \Box }$$

で表すことにする。空節が導かれれば論理式

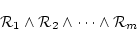$${\cal R}_1 \land {\cal R}_2 \land \cdots \land {\cal R}_m$$ (5.28)

が偽であることを示したことになる。

以上の議論から，

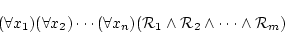$$(\forall x_1)(\forall x_2) \cdots (\forall x_n) ({\cal R}_1 \land {\cal R}_2 \land \cdots \land {\cal R}_m)$$ (5.29)

が充足不能であることを示すには，全ての解釈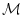${\cal M}$に対して

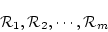$${\cal R}_1 ,{\cal R}_2 ,\cdots , {\cal R}_m$$ (5.30)

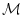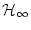に導出原理を適用して空節を導けばよいことがわかった。 さらに解釈${\cal M}$の対象領域${\bf D}$については以下のエルブラン領域 ${\cal H}_\infty$だけを調べればよいことが知られている。