


: 導出原理
: 導出原理
: スコーレム標準形
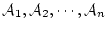 が全て個体閉論理式
として,前節まで議論によれば
が全て個体閉論理式
として,前節まで議論によれば
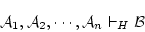 |
(5.20) |
を示すには
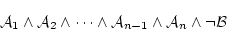 |
(5.21) |
が充足不能であることを示せばよく,この論理式はさらに
同値変形で以下のようなスコーレム標準形に変形できた。
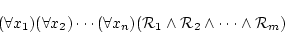 |
(5.22) |
ここで,
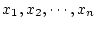 は
は
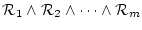 に現れる
全ての自由変数である。
また各
に現れる
全ての自由変数である。
また各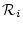 は
は
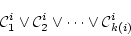 |
(5.23) |
の形で,これを節と呼ぶ。
さらに,各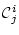 は
論理記号を含まない論理式
は
論理記号を含まない論理式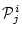 により,
により,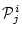 または
または
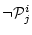 である。
これをリテラル(literal)と呼ぶ。
である。
これをリテラル(literal)と呼ぶ。
Yasunari SHIDAMA