


: 基本的な論理演算
: 記号論理
: 記号
代数でそうであったように,命題論理でも 式が定義される。
それは論理式と呼ばれる。
代数で学んだように,
は式であるが
は式でない。変数記号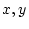 と演算記号
と演算記号 を用いて式を
作るためには決まりがあった。
同様に命題変数の記号
を用いて式を
作るためには決まりがあった。
同様に命題変数の記号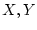 や論理演算の記号
や論理演算の記号
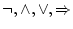 を用いて論理式を作るのにも次のような規則がある。
を用いて論理式を作るのにも次のような規則がある。
- (1).
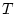 および
および 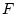 は論理式である。
は論理式である。
- (2).
- 個々の命題変数は論理式である。
- (3).
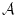 が論理式ならば、
が論理式ならば、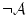 は論理式である。
は論理式である。
- (4).
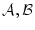 が論理式ならば、
が論理式ならば、
は、いずれも論理式である。
上の定義では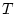 と
と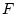 以外具体的な論理式は出てこない。
以外具体的な論理式は出てこない。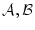 は不特定な論理式を表すメタ記号であって,具体的な論理式ではない。
しかし,これらの規則で無数の論理式を作りだすことができる。
例えば
は不特定な論理式を表すメタ記号であって,具体的な論理式ではない。
しかし,これらの規則で無数の論理式を作りだすことができる。
例えば
上の例でも判るように,プログラム言語を学んだ人には馴染みのある
「再帰的」な定義になっている。
命題論理における論理式の全体を 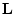 と書くことにしよう。
と書くことにしよう。
Yasunari SHIDAMA
