変分問題

変分法の典型的な問題は，第１章でも述べましたが
原点$(0,0)$と点$(1,1)$を通りその長さが最小になるような線分 $(x,f(x)), x \in [0,1]$を与える関数$f(x)$を求めよ
といった問題です。問題の関数$f(x)$を区間$[0,1]$の各点$x$で微分可能でその微分係数が$x$について連続な関数の仲間から探すとすれば，この問題は， $f(x)$による線分の長さが

$$\int_0^1\sqrt{1 + (f'(x))^2} dx$$ (2.7)

で与えられるので，この積分式を$L(f)$で表し，これを$f$が原点$(0,0)$と$(1,0)$を通るという条件

$$f(0) = 0, f(1) = 1$$

のもとに最小にする

$$f \in C^1[0,1]$$

を求めよ。と記述されます。ここで，

$$C^1[0,1]$$

は区間$[0,1]$上で連続微分可能な関数の全体の集合を表します。

$$\begin{eqnarray*} &&C^1[0,1]=\{f\vert f:[0,1]から{\bf R}へ関数,かつ,f:[0,1]上で.. ...,\\ &&その導関数x\in [0,1] \mapsto f'(x)がxについて連続。\} \\ \end{eqnarray*}$$

以後，この問題を解いていきますが，$C^1[0,1]$のような集合を関数空間と呼び， $L(f)$のように，関数空間の要素である関数$f$に実数値を対応させるものを 汎関数とよびます。上の問題では 汎関数

$$L : f \in C^1[0,1] \mapsto L(f)=\int_0^1\sqrt{1 + (f'(x))^2} dx \in {\bf R}$$

が定義されています。
変分法は汎関数の最大, 最小問題です。

見通しを良くするため，先ず以下の問題を解いてみます。
変分問題その１ 汎関数

$$L(f)=\int_0^1(f'(x))^2\,dx$$

を境界条件$f(0)=0,f(1)=1$のもとに最小にする $f \in C^1[0,1]$を求めよ。

[解法] $L(f)$は $f=f_0 \in C^1[0,1]$で最小と仮定します。
ここで

$$g \in C^1[0,1]\, , \,g(0)=0\, , \,g(1)=1$$

となる任意の $g$ をとり，

$$\Delta f(x)=g(x)-f_0(x)$$

とおくと,
$\Delta f \in C^1[0,1],\Delta f(0) = \Delta f(1) = 0$ となります。
$h \in R$をとり

$$f_h(x)=f_0(x)+h \Delta f(x)$$

とします。
$h = 0$のとき$f_h(x)=f_0(x)$となります。
ここで$L(f_h)$を

$$P(h) = L(f_h) = \int_0^1(f_h'(x))^2\,dx$$

とおきます。$P(h)$は$h = 0$で最小である。そこで補題2.1.1を適用します。

注意しなければならないのは,補題の条件は,極小値や極大値を与える必要条件ということです。 その条件を充たすものを求めたとしても,「必要条件」を充たす「候補」で,それが,「最小（最大）」 かどうかは別途調べる必要があります。

この補題2.1.1を適用するため, $P$の$h = 0$における微分可能性を示し,

$$\frac{dP}{dh}(0)$$

を求めることにします。
まず

$$P(h) = L(f_h)=\int_0^1\left(f_h'(x)\right)^2\,dx$$

$$= \int_0^1\left\{\frac{d}{dx}(f_0(x)+h \Delta f(x))\right\}^2\,dx$$

$$= \int_0^1(f_0'(x)+h \Delta f'(x))^2\,dx$$

であることに注意します。

$$\frac{dP}{dh}(0)$$

の定義は

$$\frac{d}{dh}P(0)=\lim_{h\rightarrow 0}\frac{P(h)-P(0)}{h}$$

です。右辺を計算すると,

$$\frac{P(h) - P(0)}{h} = \frac{ \int_0^1 (f_0'(x) + h \Delta f'(x))^2 \, dx - \int_0^1 (f_0'(x))^2 \,dx}{h}$$

$$= \int_0^1 \frac{1}{h} \{(f_0'(x) + h \Delta f'(x))^2 - (f_0'(x))^2 \} \,dx$$

$$= \int_0^1 \{2f_0'(x) \Delta f'(x) + h ( \Delta f'(x))^2 \} \,dx$$

$$= 2 \int_0^1 \{f_0'(x) \Delta f'(x) \} \,dx + h \int_0^1 \{ ( \Delta f'(x))^2 \} \,dx$$

となります。すなわち

$$\frac{d}{dh}P(0) = \lim_{h\rightarrow0} 2 \int_0^1 \{f_0'(x) \Delta f'(x) \} \,dx + h \int_0^1 \{ ( \Delta f'(x))^2 \} \,dx$$

$$= 2 \int_0^1 \{f_0'(x) \Delta f'(x) \} \,dx$$ (2.8)

ここで

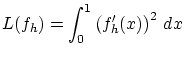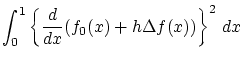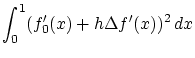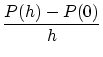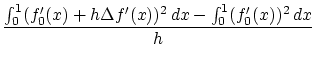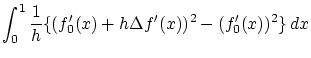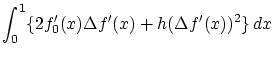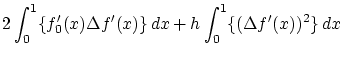[ハールの補題の適用]
補題により$P$が$h = 0$ で 微分可能で極小値をとるから

$$\frac{dP}{dh}(0) =0$$

.
すなわち

$$\int_0^1 \Delta f'(x) f_0'(x) \,dx = 0$$

となります。次に ハールの補題を適用します。
ハールの補題には幾通りかのものがありますが，ここでは その一つを挙げます。

補題 2.2.1 (ハールの補題)   $\eta$ が$[x_1,x_2]$上で連続で， $\varphi(x_1)=\varphi(x_2)=0$となるすべての $\varphi \in C^1 [x_1,x_2]$ に対して

$$\int_{x_1}^{x_2} \eta(x) \frac{d \varphi}{dx}(x) \,dx = 0$$

を満たすならば，
ある定数$\omega$が存在し

$$\eta(x) \equiv \omega,\quad x \in [x_1,x_2]$$

(証明)

$$\omega=\frac{\int_{x_1}^{x_2}\eta(x) dx }{x_2-x_1}$$

とおくと，

$$\int_{x_1}^{x_2}[\eta(x) -\omega]dx =0$$

です。ここで，

$$\varphi(x)=\int_{x_1}^x [\eta(s) -\omega]ds$$

とおくと，

$$\frac{d \varphi}{dx}(x)=\eta(x) -\omega$$

で

$$\varphi(x_1)=\int_{x_1}^{x_1}[\eta(x) -\omega]dx=0,\quad \varphi(x_2)=\int_{x_1}^{x_2}[\eta(x) -\omega]dx=0$$

です。補題の仮定から，

$$\begin{eqnarray*} \int_{x_1}^{x_2}[\eta(x) -\omega]^2 dx &=&\int_{x_1}^{x_2}[\et... ...rac{d \varphi}{dx}(x) \,dx -\omega [\varphi(x_2)-\varphi(x_1)]=0 \end{eqnarray*}$$

従って

$$\eta(x) -\omega \equiv 0 ,\quad x \in [x_1,x_2]$$

これを用いて $\Delta f(x) \in C^1 [0,1]$は任意かつ,
$\Delta f(0) = 0, \, \Delta f(1) = 0$なのである定数$C_1$が存在して，

$$f_0'(x) \equiv C_1$$

よって

$$f_0(x) = C_1 x + C_2 \quad(C_2:定数)$$

境界条件 $f_0(0) = 0 , \quad f_0(1) = 1 \,$より

$$C_1 = 1, \quad C_2 = 0$$

故に

$$f_0(x) = x$$