


: 変分問題
: 変分法
: 変分法
目次
実数値関数
が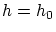 で極小(極大)であるとは,
で極小(極大)であるとは,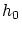 を含むある
開区間
を含むある
開区間
が存在して
この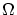 上では全ての
上では全ての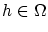 対して
対して
が成立つことを言います。要するに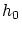 の近傍で最小(または最大)
であるという意味です。
の近傍で最小(または最大)
であるという意味です。
ここで関数
が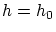 で微分可能ならば以下の必要条件が成立ちます。
で微分可能ならば以下の必要条件が成立ちます。
(証明)
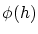 は
は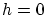 で極小であるとすると:(極大の場合も全く同じ)
で極小であるとすると:(極大の場合も全く同じ)
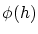 が
が 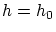 で微分可能であるとは次の極限値
で微分可能であるとは次の極限値
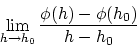 |
(2.2) |
が存在することでした。そしてこの極限値を
で表しました。
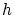 の
の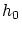 への近づき方は右から(
への近づき方は右から(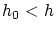 )でも左から(
)でも左から(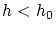 )でもよく,
2つの極限値
)でもよく,
2つの極限値
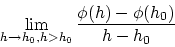 |
(2.3) |
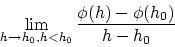 |
(2.4) |
の何れもが存在しこれらは(2.2)式に一致する。
さて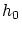 の右側で十分近い
の右側で十分近い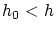 をとると,
をとると,
であり,かつ,極小の条件から
です。従って,
であり,この式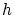 について
について
とすれば,
が得らます。この極限値は(2.2)式に一致したので,
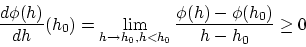 |
(2.5) |
同様に今度は反対側の左から
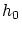 の左側で十分近い
の左側で十分近い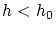 をとると,
をとると,
から
であり,この式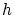 について
について
とすれば,
が得られます。この極限値は(2.2)式に一致するので,
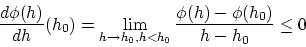 |
(2.6) |
結局,(2.5),(2.6)式から



: 変分問題
: 変分法
: 変分法
目次
Yasunari SHIDAMA
![]() の左側で十分近い
の左側で十分近い![]() をとると,
をとると,