


: 補足1:少し神経質なお話
: 変分法
: 変分問題
目次
変分問題2
さて,始めに挙げた線分の長さを最小にする問題に戻りましょう。再度,書けば,
問題 汎関数
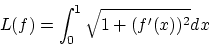 |
(2.9) |
を境界条件
のもとに最小にする
![$f \in C^1[0,1]$](img143.gif) を求めよ。
を求めよ。
[解法]
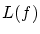 は
は
![$f=f_0 \in C^1[0,1]$](img144.gif) で最小と
仮定します。
で最小と
仮定します。
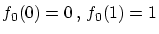
![$ g \in C^1[0,1]\, , \, g(0)=0\, , \,g(1)=1 $](img196.gif) となる任意の
となる任意の 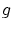 をとります。
をとります。
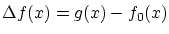 とおくと,
とおくと,
![\begin{displaymath}
\begin{array}{ll}
\Delta f \in C^2[0,1]\, , & \Delta f(0) ...
...0) = 0 \\
& \Delta f(1) = g(1) - f_0(1) = 0
\\
\end{array}\end{displaymath}](img198.gif) |
(2.10) |
となります。
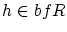 をとり
をとり
 とします。
とします。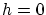 のとき
のとき
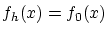 となります。
となります。
ここで  を
を
とおきます。 は
は 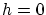 で
で
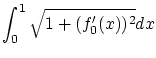 となるから最小です。そこでと問題その1と同様にして
補題1.1.1を適用します。
となるから最小です。そこでと問題その1と同様にして
補題1.1.1を適用します。
補題2.1.1(再述)
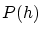 が
が 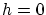 で微分可能かつ極小ならば
で微分可能かつ極小ならば
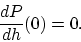 |
(2.11) |
(証明済)
この補題を適用するため,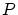 の
の 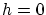 における微分可能性を
示し
における微分可能性を
示し
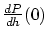 を求めることにします。
を求めることにします。
まず,
と変形します。
ところで,
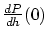 の定義は
の定義は
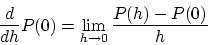 |
(2.12) |
でした。基本的には問題1と同様な計算過程を経て
を得ます。
式(2.13) 導出
式の展開を見やすくするため
とおきます。
各![$x \in [0,1]$](img210.gif) について
について
を計算すれば
となります。
式(2.13)では,極限記号と積分の記号の交換
が行われます。
このようなことは可能でしょうか?「問題その1」の場合は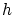 が単純に積分記号の外側
に出ていました。それでこんな心配は要らなかったわけです。
が単純に積分記号の外側
に出ていました。それでこんな心配は要らなかったわけです。
そこで,極限記号と積分記号の交換について調べてみます。これも学部1年次の微積分の
講義で習った 「一様収束」の復習です。
目標は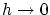 のとき
のとき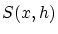 が
が
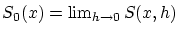 に区間
に区間![$[0,1]$](img131.gif) 上で一様収束することを示すことです。
上で一様収束することを示すことです。
この一様収束とは,任意の正数
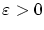 に対して,その
に対して,その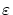 のみ
依存して決まるある正数
のみ
依存して決まるある正数
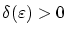 が存在して,
が存在して,
ならば 区間![$[0,1]$](img131.gif) 上の任意の
上の任意の![$x \in [0,1]$](img210.gif) に対して
に対して
が成立つことです。
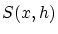 が
が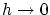 のとき
のとき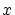 に関し一様に
に関し一様に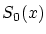 に近づくことを意味します。
に近づくことを意味します。
このとき,
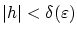 ならば,
ならば,
という評価式が得られ,
結局
すなわち,
が成立ちます。
さて,一様収束性に証明にとりかかりましょう。
先ず,![$x \in [0,1]$](img210.gif) を固定した
を固定した
は![$[0,h]$](img227.gif) 上の連続微分可能な関数であり,
上の連続微分可能な関数であり, 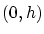 で 2 回微分可能です。
で 2 回微分可能です。
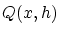 を
を 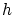 について2 次のテイラー展開をすると
について2 次のテイラー展開をすると
ただし,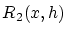 は
は
で定義されます。また に対して,
に対して,
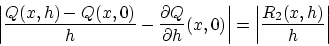 |
(2.14) |
が成立っています。
各項を計算すると,
ですから,
であり,![$x \in [0,1]$](img210.gif) に依存したある
に依存したある
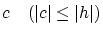 が存在して
が存在して
| |
|
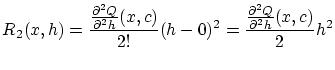 |
|
| |
|
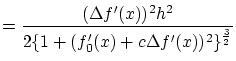 |
(2.15) |
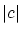 の大きさは
の大きさは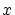 に依存していますが,
に依存していますが,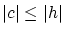 で抑えれれています。
で抑えれれています。
既に述べたように,
でした。
(2.14)より,
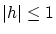 としても一般性を失わないので,
としても一般性を失わないので, 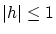 とします。
(2.15) より,
とします。
(2.15) より,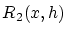 は
は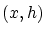 について連続です。
について連続です。
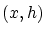 は有界な領域
は有界な領域
![$[0,1] \times [-1,1]$](img246.gif) 上を動くものとしてよいから,
ある正数
上を動くものとしてよいから,
ある正数 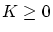 が存在して,任意の
が存在して,任意の![$x \in [0,1]$](img210.gif) と
と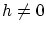 に対して
に対して
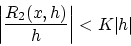 |
(2.16) |
が得られます。(2.5節の補足で証明します。)
そこで,
とおきます。
ならば,任意の![$x \in [0,1]$](img210.gif) に対して,
に対して,
よって, 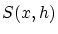 は
は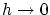 のとき
のとき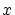 に関し一様に
に関し一様に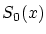 に収束します。
に収束します。
既に述べたが
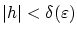 ならば,
ならば,
すなわち,
以上より,
![\begin{displaymath}
\left[ \frac{dP(h)}{dh}\right]_{h=0} =
\int_0^1\frac{f'_0(x)\Delta f'(x)}{\sqrt{1 + (f'_0(x))^2}} dx
\end{displaymath}](img251.gif) |
(2.17) |
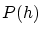 は
は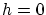 で微分可能で極小値をもつから,補題2.1.1より
で微分可能で極小値をもつから,補題2.1.1より
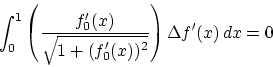 |
(2.18) |
これに問題1と同様に以下のハールの補題を適用します。
補題2.2.1(ハールの補題:再述)
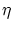 が
が![$[x_1,x_2]$](img173.gif) 上で連続で,
上で連続で,
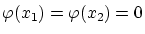 となるすべての
となるすべての
![$ \varphi \in C^1 [x_1,x_2]$](img175.gif) に対して
に対して
を満たすならば,
ある定数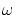 が存在し
が存在し
(証明済)
これを用いると,(2.18) において
![$ \Delta f(x) \in C^1 [0,1]$](img186.gif) は任意で,
は任意で,
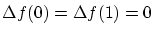 ゆえ,ある定数
ゆえ,ある定数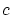 が存在して,
が存在して,
これから
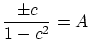 と置くと,
と置くと,
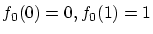 より
より
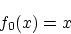 |
(2.19) |



: 補足1:少し神経質なお話
: 変分法
: 変分問題
目次
Yasunari SHIDAMA
![]() は
は
![]() で最小と
仮定します。
で最小と
仮定します。
![]()
![]() となる任意の
となる任意の ![]() をとります。
をとります。
![]() とおくと,
とおくと,
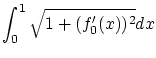 となるから最小です。そこでと問題その1と同様にして
補題1.1.1を適用します。
となるから最小です。そこでと問題その1と同様にして
補題1.1.1を適用します。
![]() が
が ![]() で微分可能かつ極小ならば
で微分可能かつ極小ならば
![]() の
の ![]() における微分可能性を
示し
における微分可能性を
示し
![]() を求めることにします。
を求めることにします。
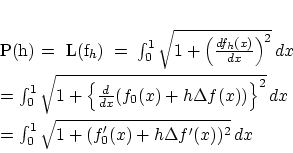
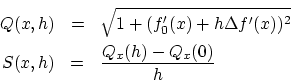
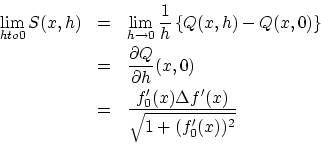
![]() のとき
のとき![]() が
が
![]() に区間
に区間![]() 上で一様収束することを示すことです。
上で一様収束することを示すことです。
![]() に対して,その
に対して,その![]() のみ
依存して決まるある正数
のみ
依存して決まるある正数
![]() が存在して,
が存在して,
![]() が
が![]() のとき
のとき![]() に関し一様に
に関し一様に![]() に近づくことを意味します。
に近づくことを意味します。
![]() ならば,
ならば,
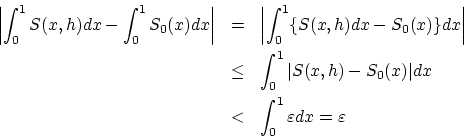
![]() を固定した
を固定した
![]() を
を ![]() について2 次のテイラー展開をすると
について2 次のテイラー展開をすると
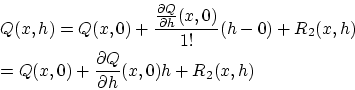
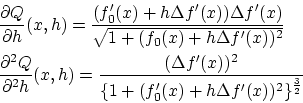
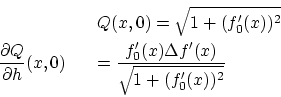
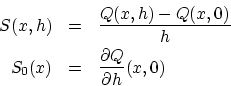
![]() ならば,
ならば,
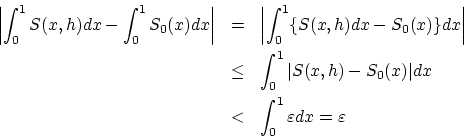
![]() は任意で,
は任意で,
![]() ゆえ,ある定数
ゆえ,ある定数![]() が存在して,
が存在して,
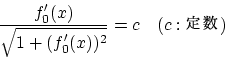
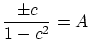 と置くと,
と置くと,