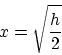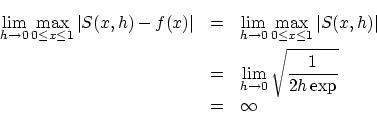


: 補足2
: 変分法
: 変分問題2
目次
補足1:少し神経質なお話
この例では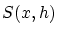 が
が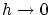 のとき
のとき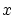 に関し一様に
に関し一様に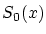 に収束することから
極限記号と積分記号の交換が可能で
に収束することから
極限記号と積分記号の交換が可能で
となりましたが,収束が一様でない場合は注意を要します。
以下の例の様に極限記号と積分記号の交換できない場合もあります。
再び,微積分の復習になります,
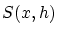 が
が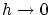 のとき
のとき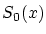 に各点収束するとは
に各点収束するとは
任意の正数
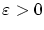 に対して,その
に対して,その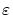 と
と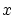 の両方に
依存して決まるある正数
の両方に
依存して決まるある正数
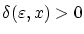 が存在して,
が存在して,
ならば
が成立つことです。
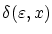 が
が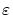 と
と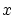 の両方に依存してきまると,
以下のように,一様収束の場合と様子が違ってきます。
の両方に依存してきまると,
以下のように,一様収束の場合と様子が違ってきます。
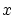 について各点収束する関数の例として
について各点収束する関数の例として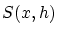 を
を
で定義します。
まず,
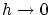 のときの
のときの
を調べておきます。
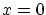 のときは
のときは
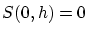 となるので
となるので
です。それ以外の![$x \in (0,1]$](img271.gif) では
では
定義から
ですので,
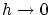 のとき
のとき
さて,この例では極限記号と積分記号の交換は可能でしょうか?
しかし一方
ゆえに
上の式のように困った事態になるのは関数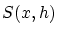 が一様収束しないからです。
一様収束するには以下の条件が必要です。
が一様収束しないからです。
一様収束するには以下の条件が必要です。
そこで
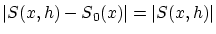 の最大値を調べてみます。
の最大値を調べてみます。
となるのは
のときで,
最大値は
となり,結局,
というように
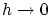 のとき無限大に発散してしまいます。
のとき無限大に発散してしまいます。
従って関数列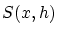 は一様収束しません。
は一様収束しません。



: 補足2
: 変分法
: 変分問題2
目次
Yasunari SHIDAMA
![]() について各点収束する関数の例として
について各点収束する関数の例として![]() を
を
![]() のときの
のときの
![]() のときは
のときは
![]() となるので
となるので
![]() のとき
のとき
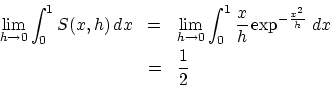
![]() が一様収束しないからです。
一様収束するには以下の条件が必要です。
が一様収束しないからです。
一様収束するには以下の条件が必要です。
![]() の最大値を調べてみます。
の最大値を調べてみます。