


: この文書について...
: 変分法
: 補足1:少し神経質なお話
目次
補足2
ところで,(2.3) がいえるためには,
と置いたとき,ある正数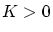 が存在して,
任意の
が存在して,
任意の
に対して
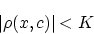 |
(2.20) |
が言えればよいことになります。
これも再び,微積分の復習になりますが,以下の定理を使います。
定理 2.5.1
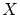
を
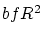
の有界閉集合,
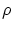
を
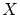
上の
連続関数とするとき,
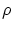
は
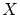
で最大値,最小値をとる。すなわち,
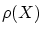
は最大値,および最小値をもつ。
先ずこの定理を用いて(2.20)を示しておきましょう。
((2.20) の証明)
![$[0, 1] \times [-1, 1] \in \\ bfR^2$](img293.gif) は有界閉集合です。
は有界閉集合です。
![$f_0 \in C^2[0, 1], \, \Delta f \in
C^2[0,1]$](img294.gif) であるから,
であるから,
.
さらに, 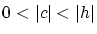 であり, 分母が
であり, 分母が
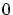 になることはなく,
になることはなく,
.
以上から,定理より 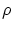 は
は
で最大値
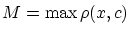 ,最小値
,最小値
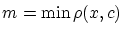 を持ちます。
よって,
を持ちます。
よって,
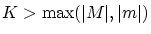 となるような
となるような 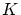 が存在します。
が存在します。
さて上の定理を順を追って証明しよう。
集積点と閉集合の定義は以下の通りです。
大抵の解析学の教科書には載っていますが,
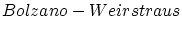 の定理を証明しておきます。
の定理を証明しておきます。
定理 2.5.2 (Bolzano-Weirstraus)
点列
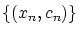
が有界であれば,その中から収束する部分列を取り出すこと
ができる。
(区間縮小法による証明)
[区間縮小の原理]
実数の単調増加列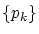 と単調減少列
と単調減少列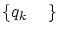 により 区間の列
により 区間の列![$[p_k, q_k]$](img310.gif) を構成し,その区間の長さが
を構成し,その区間の長さが
のように縮小すると,
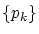 ,
,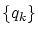 の極限
の極限
が存在して
となります。これを用いて定理を証明します。
まず,有界な数列 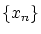 から収束する部分列をと
りだすことができることを示します。
から収束する部分列をと
りだすことができることを示します。
数列 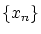 が有界ならば,
が有界ならば,
となる 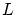 が存在します。
が存在します。
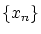 の中に同じ数が無限回現れるときは,その
番号を次々に取り出して
の中に同じ数が無限回現れるときは,その
番号を次々に取り出して
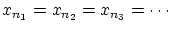 とできます。
とできます。
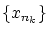 は明らかに収束列です。したがって,はじめから
は明らかに収束列です。したがって,はじめから 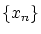 の中には相異なる数が無限個存在するとして良いわけです。
の中には相異なる数が無限個存在するとして良いわけです。
そうしておくと,区間
![$[-L, 0], \, [0, L]$](img319.gif) のうち少なくとも一方は
のうち少なくとも一方は
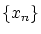 の(相異なる)元を無限個含みます。
の(相異なる)元を無限個含みます。
それを 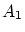 とおきます。
とおきます。
に含まれる 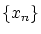 の元を一つ取って,
それを
の元を一つ取って,
それを 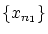 といます。
といます。
次に,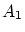 を二つの部分
を二つの部分
に分けると,少なくとも一方は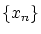 の元を無限個含むことになります。
の元を無限個含むことになります。
それを
とおきます。
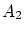 に含まれる
に含まれる 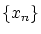 の元で
の元で 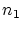 より大きい番号のものを一つ取りだし,それを
より大きい番号のものを一つ取りだし,それを
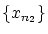 とします。
とします。
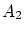 を二つの部分
を二つの部分
に分けます。
以下同様の手続きを繰り返します。
これを続けることにより,次のような閉区間の列
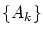 と
と 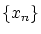 の部分列
の部分列 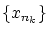 を作ることができます。
を作ることができます。
-
![$A_k = [p_k, q_k]$](img330.gif) とおくと,
とおくと,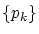 は単調増加列,
は単調増加列,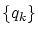 は単調減少列で
は単調減少列で
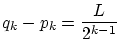
-
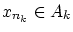 ,すなわち
,すなわち
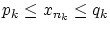
実数の有界な単調列は収束しますから,
が存在します。
上の 1. より
です。
2. より
を得ます。
さて,実数列
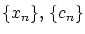 は有界でしたから,ま
ず 上の議論により,
は有界でしたから,ま
ず 上の議論により,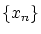 から収束する部分列が取り出せます。
から収束する部分列が取り出せます。
それを 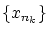 で表し
で表し
とおきます。
次に,全く同様に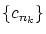 も有界ですから収束する部分列が取り出せるので,
それを
も有界ですから収束する部分列が取り出せるので,
それを
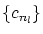 であらわし,
であらわし,
とおきます。
すると
となります。
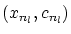 は
は 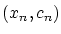 の部分列であって,
の部分列であって,
です。
よって,
です。
集合論のWEB教材でも説明しましたが,
以上の準備の下に,
定理 2.5.3
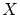
を
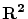
の有界閉集合,
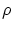
を
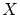
上の
連続関数とする。このとき,
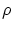
は
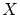
で最大値,最小値をとる。すなわち,
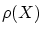
は最大値,および最小値をもつ。
(証明)まず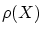 は有界です。実際,
は有界です。実際,
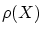 が有界でなかったとすると,
が有界でなかったとすると,
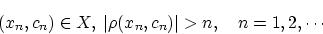 |
(2.21) |
となる数列
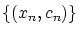 がとれます。
がとれます。
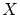 は有界閉集合ですから,,
は有界閉集合ですから,,
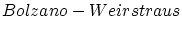 の定理によって
の定理によって
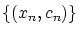 は収束する部分列を含み,かつその極限値もまた
は収束する部分列を含み,かつその極限値もまた
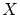 に属します。
に属します。
その一つを
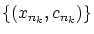 とおき,
とおき,
とおくと,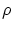 の連続性より
の連続性より
.
ところが一方,(2.21) より,
.
が成り立っていてこれは矛盾です。
さて以上によって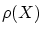 は有界でしたから,
は有界でしたから,
となる
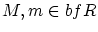 があります。
があります。
この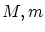 が
が
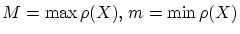 となることを示しましょう。
となることを示しましょう。
まず,上限の定義から
となるような 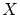 の元からなる数
列
の元からなる数
列
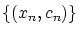 がとれます。
がとれます。
この列はに収束しますから,有界です。
そこで,
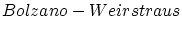 の定理によって
の定理によって
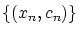 から収束する部分列
から収束する部分列
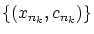 をとりだし,
をとりだし,
とすると,
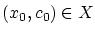 であり
であり 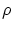 の連
続性から
の連
続性から
となります。
ゆえに,
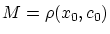 .よって
.よって  は最大値
です。最小値の場合も同様です。
は最大値
です。最小値の場合も同様です。



: この文書について...
: 変分法
: 補足1:少し神経質なお話
目次
Yasunari SHIDAMA
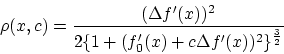
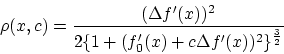
![]() は有界閉集合です。
は有界閉集合です。
![]() であるから,
であるから,
![]() と単調減少列
と単調減少列![]() により 区間の列
により 区間の列![]() を構成し,その区間の長さが
を構成し,その区間の長さが
![]() から収束する部分列をと
りだすことができることを示します。
から収束する部分列をと
りだすことができることを示します。
![]() が有界ならば,
が有界ならば,
![]() は明らかに収束列です。したがって,はじめから
は明らかに収束列です。したがって,はじめから ![]() の中には相異なる数が無限個存在するとして良いわけです。
の中には相異なる数が無限個存在するとして良いわけです。
![]() のうち少なくとも一方は
のうち少なくとも一方は
![]() の(相異なる)元を無限個含みます。
の(相異なる)元を無限個含みます。
![]() とおきます。
とおきます。
![]() を二つの部分
を二つの部分
![]() と
と ![]() の部分列
の部分列 ![]() を作ることができます。
を作ることができます。
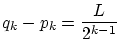
![]() は有界でしたから,ま
ず 上の議論により,
は有界でしたから,ま
ず 上の議論により,![]() から収束する部分列が取り出せます。
から収束する部分列が取り出せます。
![]() で表し
で表し
![]() は
は ![]() の部分列であって,
の部分列であって,
![]() は有界閉集合ですから,,
は有界閉集合ですから,,
![]() の定理によって
の定理によって
![]() は収束する部分列を含み,かつその極限値もまた
は収束する部分列を含み,かつその極限値もまた
![]() に属します。
に属します。
![]() とおき,
とおき,
![]() は有界でしたから,
は有界でしたから,
![]() が
が
![]() となることを示しましょう。
となることを示しましょう。