さて,![]() やそれから作られる
やそれから作られる![]() 次元数ベクトル空間
次元数ベクトル空間![]() については
線形空間であるという性質以外に絶対値やノルムが定義されていました。
これも復習しておきます。
については
線形空間であるという性質以外に絶対値やノルムが定義されていました。
これも復習しておきます。
![]() についてはその要素
についてはその要素
![]() に対して絶対値とよばれる負でない数
に対して絶対値とよばれる負でない数![]() が対応して
が対応して
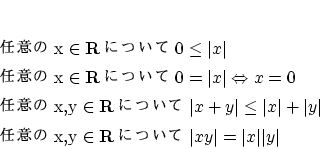
同様に![]() の要素
の要素![]() についても
についても![]() での絶対値のように
ノルムと呼ばれる負でない数
での絶対値のように
ノルムと呼ばれる負でない数![]() が対応して
が対応して
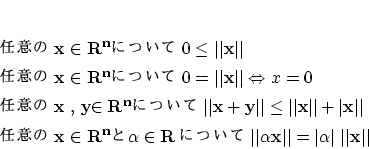
![]() の要素
の要素
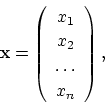
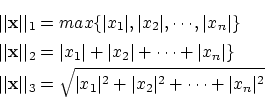
[問題3.3]
上の3つが何れもノルムを定義することを確かめてください。また,
実数値関数
[例1]
例1
![]() のノルムを
のノルムを
(証明)
(1.4)式より明らかに
![]() また
また![]() ならば
ならば![]()
そして![]() ならば
ならば
例2
![]() のノルムを
のノルムを
(証明)
(1.7)式より明らかに
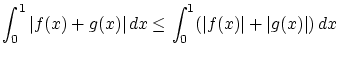 |
|||
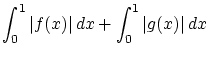 |
|||
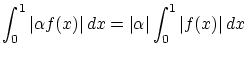 |
|||
例3
![]() は以下のノルムで,ノルム線形空間になります。
は以下のノルムで,ノルム線形空間になります。
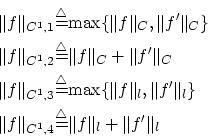
[問題3.4] 上を証明してください。