


: 定義
: 写像
: 写像
目次
関数とか写像というのは,中学・高校時代から習っていています.
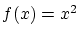 とか
とか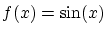 です.
です.
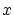 に
に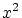 を対応させる関数を
を対応させる関数を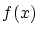 とする.
とする.
というように使うのですが,写像や関数は対象と対象を対応させる
機能や規則を表していて,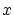 とか
とか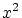 と違い具体的な対象ではないようにみえます.
と違い具体的な対象ではないようにみえます.
しかし,これも,数と同じように対象の一つとして扱います.
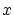 から
から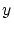 への写像とか関数と呼ばれるものを数と同じように扱うことができるような定義を与えておきます. (これが唯一の方法ということではありません.)
への写像とか関数と呼ばれるものを数と同じように扱うことができるような定義を与えておきます. (これが唯一の方法ということではありません.)
材料は写像の定義域の集合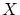 ,値域の集合
,値域の集合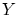 ,それに
,それに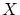 の要素
の要素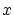 に
に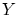 の要素
の要素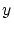 を対応させる規則です.
を対応させる規則です.
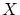 から
から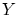 への写像(あるいは関数)
への写像(あるいは関数)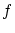 は形式的に
は形式的に
という3重の対として定義されます.
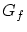 は写像
は写像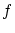 のグラフと呼ばれます.これは,
のグラフと呼ばれます.これは,
の部分集合,つまり
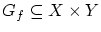 で,任意の
で,任意の
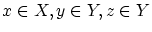 について
について
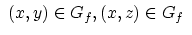 なら
なら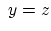 になるものです.
になるものです.
また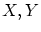 と
と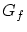 には
には
が成り立つという条件を課します.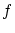 のグラフ
のグラフ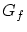 は,
例えば
は,
例えば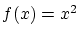 についてその曲線を座標に書くと判りますように
曲線上の点
についてその曲線を座標に書くと判りますように
曲線上の点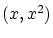 全ての集合で文字通りグラフ
全ての集合で文字通りグラフ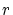 です.
です.
以上の定義を記号論理で書けば
Yasunari SHIDAMA