


: 集合族
: 写像の形式的定義
: 定義
目次
前節では,集合の直積を用いて写像を以下のように形式的に定義しました。
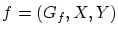 が
が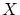 から
から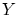 への写像
への写像
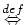
しかし,この定義では写像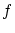 のグラフ
のグラフ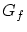 の具体的な構成法については述べられていません。
例えば,実数空間
の具体的な構成法については述べられていません。
例えば,実数空間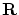 の元
の元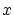 にその絶対値
にその絶対値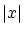 を対応させる写像
を対応させる写像
を構成することを考えましょう。
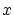 には
には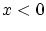 のとき
のとき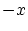 が,
が,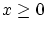 のとき
のとき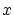 が一意に対応します。
が一意に対応します。
関係式
を
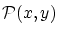 とおくと
とおくと
が成立つます。第2章の議論により
という集合が定義できます。これが写像のグラフを定義していることを確かめるのは
容易です。
一般に関係式
について
と
が成立つとき
という集合が定義でき,写像のグラフを定義します。
Yasunari SHIDAMA
![]() が
が![]() から
から![]() への写像
への写像
![]()
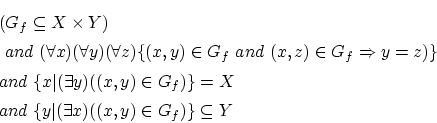
![]() のグラフ
のグラフ![]() の具体的な構成法については述べられていません。
例えば,実数空間
の具体的な構成法については述べられていません。
例えば,実数空間![]() の元
の元![]() にその絶対値
にその絶対値![]() を対応させる写像
を対応させる写像
![\begin{eqnarray*}
&&(\forall x)(\forall y)(\forall w)
(
[\{x \in {\bf R} ~and...
...} ~and~y \in {\bf R} ~and~ {\cal P}(x,w) \}
] \Rightarrow y=w)
\end{eqnarray*}](img56.png)
![\begin{eqnarray*}
&&(\forall x)(\forall y)(\forall w)
(
[\{x \in X ~and~y \in...
...x \in X ~and~y \in Y ~and~ {\cal P}(x,w) \}
] \Rightarrow y=w)
\end{eqnarray*}](img60.png)