


: 順序関係
: 関係
: 商集合
目次
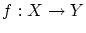 とします.
とします.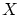 上の同値関係
上の同値関係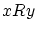 を
を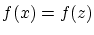 で定義します.
で定義します.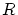 の直積による表現は
の直積による表現は
です.
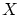 から
から
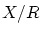 への写像
への写像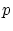 を
を
で定義します.
このとき
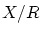 から
から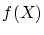 への写像
への写像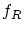 が
が
で定義され,これは双射で
ここで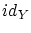 は
は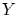 上の恒等写像
上の恒等写像
という関係が成り立っています.これを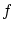 の標準分解と言います.
の標準分解と言います.
[証明]
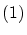 まず,
まず,
が写像を定義していることを確認します.すなわち
が写像になっていることを確認します.
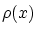 は
は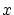 と
と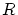 について同値な
について同値な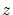 によって
によって
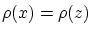 となります.
となります.
この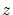 は
は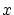 と等しいとは限りません.代表元の取り方が異なるわけです.
と等しいとは限りません.代表元の取り方が異なるわけです.
しかし,この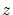 を用いて
を用いて
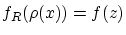 としても,
としても,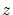 は
は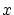 と
と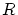 について同値ゆえ
について同値ゆえ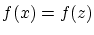 となります. 結局
となります. 結局
が成り立っています.
として
で
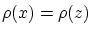 なら
なら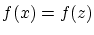 が成り立っていますので
が成り立っていますので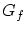 は関数のグラフになっています.
は関数のグラフになっています.
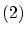 次に,
次に,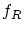 が全射であることを確認します.
が全射であることを確認します.
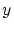 が
が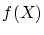 の元ならある
の元ならある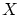 の元
の元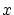 が存在して
が存在して
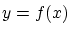 です.
です.
この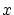 の同値類
の同値類
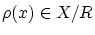 に
に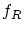 を作用させれば
を作用させれば
です.
即ち,
これは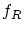 であることを示しています.
であることを示しています.
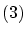 今度は,
今度は,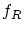 が単射であることを確認します.
が単射であることを確認します.
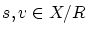 を任意にとり
を任意にとり
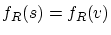 とすると
とすると
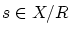 ですから,ある
ですから,ある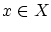 が存在して,
が存在して,
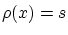
同様に 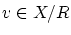 ですから,
ですから,
ある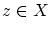 が存在して,
が存在して,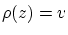
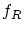 の定義から
の定義から
これらと
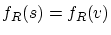 から
から
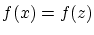
よって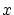 と
と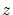 は関係
は関係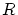 について同値.
について同値.
従って
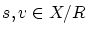 を任意にとっていましたから
を任意にとっていましたから
これは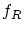 が単射であることを示しています.
が単射であることを示しています.
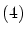 最後に
最後に
任意の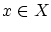 について
について
が成り立っています.
よって,
[証明終]
問題
(1)
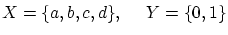 とします.
とします.
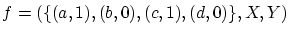
の標準分解を求めてください.
(2)
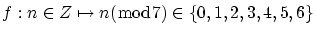
の標準分解を求めてください.
 は
は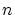 を
を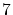 で割った余りを表します.
で割った余りを表します.



: 順序関係
: 関係
: 商集合
目次
Yasunari SHIDAMA
![]() から
から
![]() への写像
への写像![]() を
を
![]() から
から![]() への写像
への写像![]() が
が
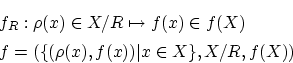
![]() であることを示しています.
であることを示しています.
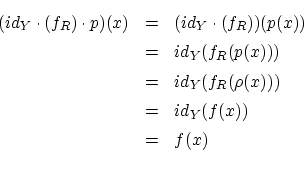
![]() とします.
とします.
![]()
![]()
![]() は
は![]() を
を![]() で割った余りを表します.
で割った余りを表します.