既述の体系![]() についてその公理系
についてその公理系![]() に論理式
に論理式
を追加してできる新たな系で 論理式
で表す。さらにこのとき:
が成り立つ。 また,これを繰り返せば
を追加してできる新たな系を
を追加してできる系を
は
であることを表している。示すべきことは
である。
が
- (1).
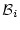 は
は
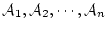 のうち1つで
ある。
のうち1つで
ある。
- (2).
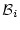 は公理系
は公理系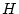 の各公理の形の論理式である。
の各公理の形の論理式である。
- (3).
- 論理式
 の前に論理式
の前に論理式 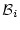 と
と
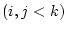 があり,
があり, は
は
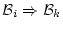 の
形をしている。
の
形をしている。
そして,
は
- (1).
 が
が
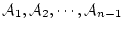 のうち1つであれば,「添加」
のうち1つであれば,「添加」
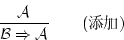
により,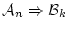 は
は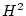 で証明可能な論理式になる。
で証明可能な論理式になる。
 が
が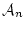 自身ならば,公理
自身ならば,公理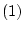 により,
により,
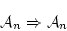
は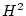 で証明可能な論理式である。
で証明可能な論理式である。
- (2).
 が公理系
が公理系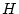 の各公理の形の論理式であるとき,
同様に「添加」により,
の各公理の形の論理式であるとき,
同様に「添加」により,
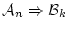 は
は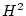 で証明可能な論理式である。
で証明可能な論理式である。
- (3).
- 論理式
 の前に論理式
の前に論理式 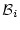 と
と
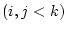 があり,
があり, は
は
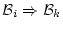 の
形をしているときは,
の
形をしているときは,
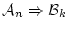 の前に,
の前に,
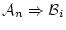 と
と
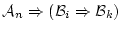 とがあることになる。
これに「復推移」
とがあることになる。
これに「復推移」
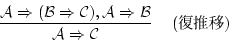
を適用すると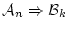 が得られる。
が得られる。
のとき
これは,まず
から演繹定理により
が得られ,これと公理
となる。さらに公理
と公理
が得られる。また,公理
が成り立っている。これらより結局
上の結果を推論規則の形で表現すれば
また論理式の形で表せば
である。(いずれも
まず,