

: 束縛変数と自由変数
: 述語論理
: 述語の論理和・論理積・否定
 変数命題関数
変数命題関数 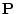
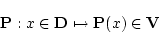 |
(3.5) |
が与えられたとき,命題
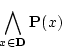 |
(3.6) |
を
で表そう。ここで
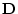 が有限個の要素からなる場合,すなわち
が有限個の要素からなる場合,すなわち
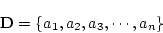 |
(3.7) |
の場合は
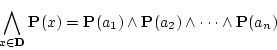 |
(3.8) |
であり, が無限集合の場合は
が無限集合の場合は
 の要素
の要素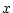 について
について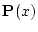 の総てに亘る論理積を表している。
の総てに亘る論理積を表している。
この命題の真理値は,
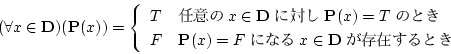 |
(3.9) |
となる。
領域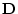 が明白なときは
が明白なときは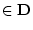 を省略する。
を省略する。
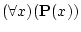 は「任意の(すべての)
は「任意の(すべての) 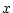 に対し
に対し 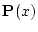 が
成立する」ことを表している。
が
成立する」ことを表している。
また
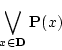 |
(3.10) |
を
で表そう。ここで
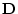 が有限個の要素からなる場合,すなわち
が有限個の要素からなる場合,すなわち
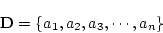 |
(3.11) |
の場合は
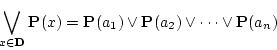 |
(3.12) |
であり,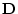 が無限集合の場合
は
が無限集合の場合
は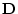 の要素
の要素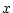 について
について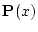 の総て
の論理和である。
この命題の真理値は
の総て
の論理和である。
この命題の真理値は
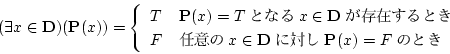 |
(3.13) |
である。上と同様に領域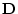 が明白なときは
が明白なときは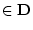 を省略する。
を省略する。
は「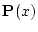 を満たす
を満たす 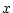 が存在する」こと
を表わしている。
が存在する」こと
を表わしている。
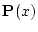 が1変数の述語の場合は,
が1変数の述語の場合は,
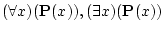 はともに
はともに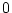 変数の述語,すなわち命題になることに
注意しておく。
変数の述語,すなわち命題になることに
注意しておく。
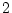 変数の述語に
変数の述語に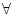 や
や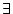 を作用させれば
を作用させれば
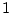 変数の述語になる。
変数の述語になる。
例えば,
を2変数の述語とすれば
| |
|
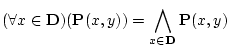 |
(3.14) |
| |
|
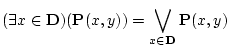 |
(3.15) |
は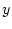 についての
についての 変数の述語になっている。
変数の述語になっている。
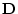 が有限集合
が有限集合
の場合なら,このことはさらに判りやすくなる。実際,
| |
|
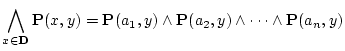 |
(3.16) |
| |
|
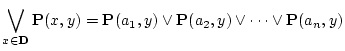 |
(3.17) |
で
は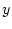 についての
についての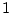 変数の述語であり,それらの論理積,論理和も
変数の述語であり,それらの論理積,論理和も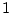 変数の述語で
ある。
変数の述語で
ある。
同様に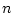 変数の述語に
変数の述語に 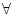 や
や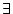 を作用させると
を作用させると
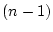 変数の述語になる。
変数の述語になる。
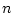 変数の述語
変数の述語
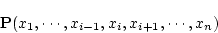 |
(3.18) |
について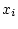 について
について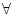 や
や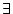 を作用させれば
を作用させれば
| |
|
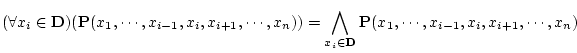 |
(3.19) |
| |
|
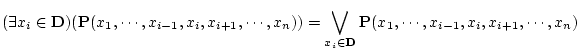 |
(3.20) |
は
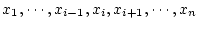 についての
についての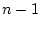 変数の述語になっている。
変数の述語になっている。
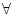 を全称記号(universal quantifire),
を全称記号(universal quantifire),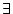 を
存在記号(existential quantifire)と呼び,両者をあわせて
限定記号という。
を
存在記号(existential quantifire)と呼び,両者をあわせて
限定記号という。


: 束縛変数と自由変数
: 述語論理
: 述語の論理和・論理積・否定
Yasunari SHIDAMA
![]() 変数命題関数
変数命題関数 ![]()
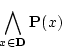
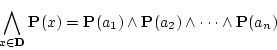
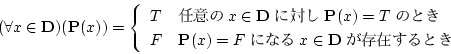
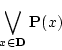
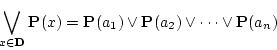
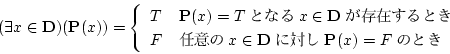
![]() が1変数の述語の場合は,
が1変数の述語の場合は,
![]() はともに
はともに![]() 変数の述語,すなわち命題になることに
注意しておく。
変数の述語,すなわち命題になることに
注意しておく。
![]() 変数の述語に
変数の述語に![]() や
や![]() を作用させれば
を作用させれば
![]() 変数の述語になる。
変数の述語になる。
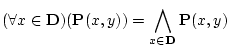
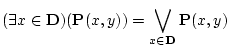
![]() が有限集合
が有限集合
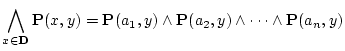
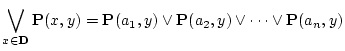
![]() 変数の述語に
変数の述語に ![]() や
や![]() を作用させると
を作用させると
![]() 変数の述語になる。
変数の述語になる。
![]() 変数の述語
変数の述語
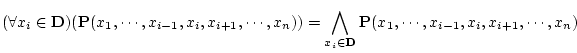
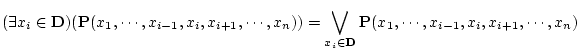
![]() を全称記号(universal quantifire),
を全称記号(universal quantifire),![]() を
存在記号(existential quantifire)と呼び,両者をあわせて
限定記号という。
を
存在記号(existential quantifire)と呼び,両者をあわせて
限定記号という。