


: 基本的な性質
: 述語論理
: 限定記号
| |
|
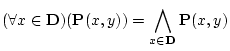 |
(3.21) |
| |
|
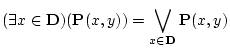 |
(3.22) |
あるいは
 が有限集合
が有限集合
の場合の,
| |
|
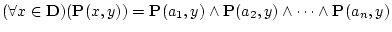 |
(3.23) |
| |
|
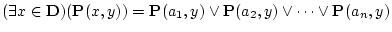 |
(3.24) |
の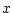 は見かけ上の変数にすぎない。このような変数を束縛変数(bound variable)と呼ぶ。束縛変数に対象を代入することはできない。
これとは逆に
は見かけ上の変数にすぎない。このような変数を束縛変数(bound variable)と呼ぶ。束縛変数に対象を代入することはできない。
これとは逆に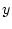 のような本来の意味の変数
を自由変数(free variable)という。自由変数には対象を代入すること
ができる。
のような本来の意味の変数
を自由変数(free variable)という。自由変数には対象を代入すること
ができる。
述語 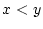 は2変数の述語であったが,
は2変数の述語であったが,
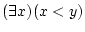 や
や
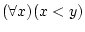 は
は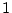 変数の述語であり,
変数の述語であり,
は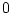 変数の述語,すなわち命題である。
変数の述語,すなわち命題である。
Yasunari SHIDAMA
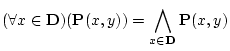
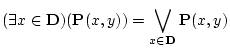
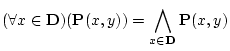
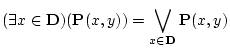
![]() が有限集合
が有限集合
![]() は2変数の述語であったが,
は2変数の述語であったが,
![]() や
や
![]() は
は![]() 変数の述語であり,
変数の述語であり,