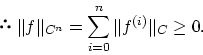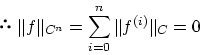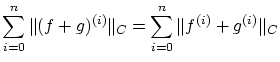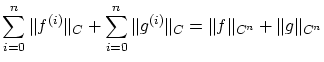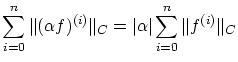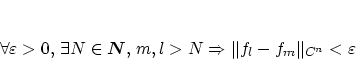


: この文書について...
: 関数空間
: ノルム線形空間
目次
定義 1.3.1
を線形空間とし,
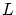
上に実数値関数
が定義され,
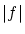
が次の条件をみたすとき
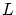
をノルム(線形)空間と定義しました。
このノルムは実数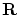 の絶対値
の絶対値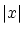 の一般化です。
さらにこれを用いて実数の集合
の一般化です。
さらにこれを用いて実数の集合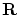 や数ベクトル空間
や数ベクトル空間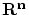 の「完備性」の一般化が可能になります。
の「完備性」の一般化が可能になります。
定義 1.3.2 (Caushy列)
ノルム空間
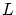
の点列
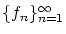
がCaushy列(あるいは基本列)
であるとは,
が成り立つことです。
定義 1.3.3
ノルム線形空間
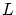
の任意のCaushy列が収束するとき,
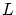
は完備(complete)であるといいます。
定義 1.3.4
完備なノルム線形空間をBanach空間といいます。
例1
![$f \in C[0,1]$](img143.gif) のノルムを
のノルムを
![\begin{displaymath}
\Vert f\Vert _C \mbox{$\stackrel{\triangle}{=}$}\max_{x \in [0,1]}\vert f(x)\vert
\end{displaymath}](img144.gif) |
(1.4) |
で定義するとBanach空間になります。
(証明)
ノルム線形空間であるは前節で証明しました。
完備性を示します。
関数列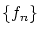 がCaushy列と仮定すると,
がCaushy列と仮定すると,
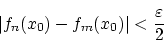 |
(1.5) |
です。すなわち任意の![$x_0 \in [0,1]$](img99.gif) に対して
に対して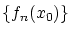 は
は
Caushy列です。従って実数の完備性により
が存在して,
とおくと![$f \in C[0,1]$](img143.gif) です。
です。
(証明)
これらより
![$f_n \in C[0,1]$](img190.gif) だから
だから
したがって
ゆえに![$f \in C[0,1]. $](img194.gif)
(例1の証明の続き)
よって
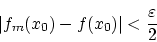 |
(1.6) |
(1.5),(1.6)より
以上より
これより
よって
 のとき
のとき
ゆえにCaushy列がつねに収束するので完備です。
例2
![$f \in C[0,1]$](img143.gif) のノルムを
のノルムを
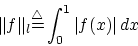 |
(1.7) |
と定義するとノルム空間になるがBanach空間にはなりません。
(証明)
ノルム線形空間であることは前節を示しました。
完備でないことを示します。
![$f_n(x) \in C[0,1]$](img210.gif) を
を
とおけば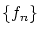 はこの空間でのCaushy列になりますが,その関数列の極限になっているような連続関数はありません。
したがって完備ではありません。
はこの空間でのCaushy列になりますが,その関数列の極限になっているような連続関数はありません。
したがって完備ではありません。
例3
![$f \in C^1[0,1]$](img172.gif) のノルムを
のノルムを
と定義するとBanach空間になります。これを証明する前に次の定理を示します。
定理 1.3.1
![$f_n \in C^1[0,1]$](img213.gif)
の導関数
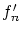
からなる関数列
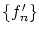
が一様収束するとする。
さらに,
![$c \in [0,1]$](img216.gif)
に対して
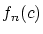
は収束するとする。
このとき
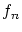
からなる関数列
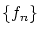
は一様収束し,かつ極限関数
は連続微分可能で,関係式
![\begin{displaymath}
\forall x \in[0,1],\, \{\lim_{n \rightarrow \infty}f_n(x)\}'
= \lim_{n \rightarrow \infty}f'_n(x)
\end{displaymath}](img220.gif) |
(1.8) |
が成り立つ。
(証明)
数列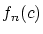 が収束することから
が収束することから
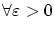 に対して
に対して
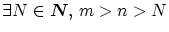 ならば
ならば
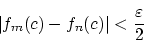 |
(1.9) |
また,関数列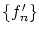 が一様収束することから,
が一様収束することから,
同一の
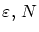 について
について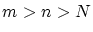 ならば
ならば
![$\forall x \in [0,1]$](img226.gif) に対して
に対して
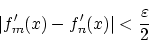 |
(1.10) |
となる。
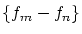 に平均値定理を適用すると,
に平均値定理を適用すると,
![$\forall x \in [0,1]$](img226.gif) に対して
に対して
したがって(1.9),(1.10)により
以上より,
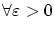 に対して
に対して
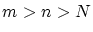 ならば
ならば
となるような,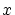 に無関係である
に無関係である
が存在します。
すなわち,関数列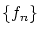 は一様収束します。
したがって,
は一様収束します。
したがって,
が存在します。
関数列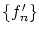 は一様収束するので
は一様収束するので
ところで,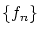 と
と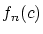 は収束するから
は収束するから
関数列 が一様収束し,各関数 が連続であるから,極限関数 は連続です。
したがって,右辺は連続関数の不定積分として連続微分可能です。
ゆえに,右辺は連続微分可能であって,微分すると
となります。
(例3の証明)
まずノルム空間であることを示します。
例1より
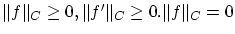 のとき
のとき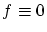 ゆえに
ゆえに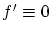
以上より(正値性),(スカラー倍),(三角不等式)が示されノルム空間となります。
次に完備性を示します。
![$f_n \in C^1[0,1]$](img213.gif) からなる関数列
からなる関数列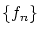 がCaushy列と仮定すると,
がCaushy列と仮定すると,
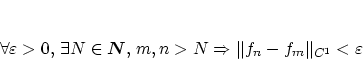 |
(1.11) |
式(1.11)より
とできます。すなわち
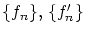 はCaushy列です。まず
はCaushy列です。まず
が存在します。すなわち
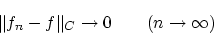 |
(1.12) |
同様に
が存在しかつ![$f' \in C[0,1]$](img253.gif) です。すなわち
です。すなわち
定理2.1より
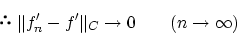 |
(1.13) |
(1.12),(1.13)より
ゆえにCaushy列がつねに収束するので完備です。
例4
![$f \in C^n[0,1]$](img261.gif) のノルムを
のノルムを
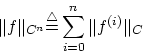 |
(1.14) |
で定義するとBanach空間になります。
(証明)
まずノルム空間であることを示します。
例3と同様に
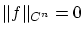 ならば(正値性)と(1.14)より
ならば(正値性)と(1.14)より .
.
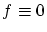 ならば
ならば
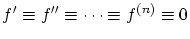
以上より(正値性),(スカラー倍),(三角不等式)が示されノルム空間となります。
次に完備性を示します。
帰納法を用いることにして![$C^{n-1}[0,1]$](img274.gif) がBanach空間であるとします。そして,
例3同様に
がBanach空間であるとします。そして,
例3同様に
![$f_l \in C^n[0,1]$](img275.gif) からなる関数列
からなる関数列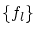 がCaushy列と仮定すると,
がCaushy列と仮定すると,
ゆえに,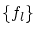 は
は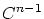 のCaushy列です。
のCaushy列です。
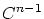 をBanach空間と仮定したので,
をBanach空間と仮定したので,
同様に,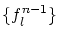 は
は![$C^1[0,1]$](img95.gif) のCaushy列であるから例3より,
のCaushy列であるから例3より,
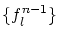 は
は![$C^1[0,1]$](img95.gif) のBanach空間になります。
のBanach空間になります。
ここで(1.16),(1.17)より,
ノルムの正値性より
![$g\in C^1[0,1]$](img14.gif) より
より
![$f^{n-1} \in C^1[0,1]$](img295.gif)
(1.15),(1.18)より
以上より完備性が示されました。



: この文書について...
: 関数空間
: ノルム線形空間
目次
Yasunari SHIDAMA
![]() の絶対値
の絶対値![]() の一般化です。
さらにこれを用いて実数の集合
の一般化です。
さらにこれを用いて実数の集合![]() や数ベクトル空間
や数ベクトル空間![]() の「完備性」の一般化が可能になります。
の「完備性」の一般化が可能になります。
![]() のノルムを
のノルムを
![]() がCaushy列と仮定すると,
がCaushy列と仮定すると,
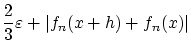
![]() のノルムを
のノルムを
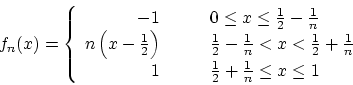
![]() のノルムを
のノルムを
![]() が収束することから
が収束することから
![]() に対して
に対して
![]() ならば
ならば
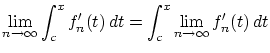
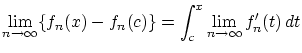
![]() のとき
のとき![]() ゆえに
ゆえに![]()
![]() のノルムを
のノルムを