


: ノルム線形空間
: 最適化理論-変分法と微分その2-
: 目次
目次
再び最初に扱った変分問題に戻りましょう。
それは汎関数
を条件
で最小化(極小化)するものでした。
解法の手順は,まず,
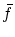 がこの問題の極小解を与えるものとして,
がこの問題の極小解を与えるものとして,
を任意に選び,
とおくと
であり,
として,
とすると,実数値関数
が定義され 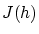 は
は 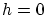 で 極小になりました。
これから
で 極小になりました。
これから
得て,ハールの補題を適用した。
これは![$g\in C^1[0,1]$](img14.gif) を介在させて,
を介在させて,
に沿った,
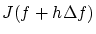 の
の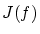 からの変動を計算したことになります。
からの変動を計算したことになります。
ここで,関数の集合
から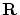 への写像
への写像
について何らかの意味の微分の概念を導入し
実数値関数の極小条件
のような扱いはできないものでしょうか?
よく知られるように実数値関数
の 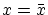 での
での
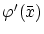 は
は
で定義されています。
これと同様な考えかたと定義を関数の集合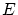 上の関数
上の関数
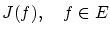 に持ち込もうというのです。
に持ち込もうというのです。
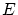 の要素間に―演算や極限操作を行うための距離―など実数の集合
の要素間に―演算や極限操作を行うための距離―など実数の集合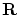 やそれから作られる
やそれから作られる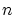 次元数ベクトル空間
次元数ベクトル空間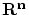 と同じような
性質が定義されている必要があるでしょう。
と同じような
性質が定義されている必要があるでしょう。



: ノルム線形空間
: 最適化理論-変分法と微分その2-
: 目次
目次
Yasunari SHIDAMA
![]() がこの問題の極小解を与えるものとして,
がこの問題の極小解を与えるものとして,
![]() を介在させて,
を介在させて,
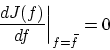
![]() の要素間に―演算や極限操作を行うための距離―など実数の集合
の要素間に―演算や極限操作を行うための距離―など実数の集合![]() やそれから作られる
やそれから作られる![]() 次元数ベクトル空間
次元数ベクトル空間![]() と同じような
性質が定義されている必要があるでしょう。
と同じような
性質が定義されている必要があるでしょう。