


: 充足性とモデル
: 述語論理の公理系
: 演繹定理
述語論理は対象領域 が具体的に与えられて初めて具体的な意味をもつ。
述語の真理値も決定される。
が具体的に与えられて初めて具体的な意味をもつ。
述語の真理値も決定される。
前節で定義された項と論理式は, 特定の対象を表す記号である対象定数記号, 上の変数を表す対象変数記号,
上の変数を表す対象変数記号,  から
から への関数を表す関数記号および
への関数を表す関数記号および 上の述語を表す述語記号から作られた記号列に過ぎない。
上の述語を表す述語記号から作られた記号列に過ぎない。
これらの記号列が3.1節で与えた対象領域上の特定の述語と,述語の論理演算として真理値を確定するためには,以下の対応を与える必要がある。
- 対象変数記号と
 の要素との対応
の要素との対応
これを
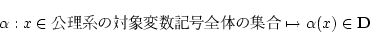 |
(4.44) |
で表す。
- 対象定数記号と
 の要素との対応
の要素との対応
対象定数記号は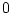 関数記号とみなし, 関数記号と
関数記号とみなし, 関数記号と
 上の関数との対応の特別な場合に含める。
上の関数との対応の特別な場合に含める。
- 関数記号と
 上の関数との対応
上の関数との対応
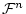 で
で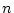 変数の関数記号の全体を,
変数の関数記号の全体を,
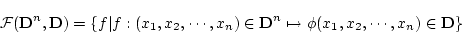 |
(4.45) |
を 上の関数全体の集合とし,これらの間の対応を
上の関数全体の集合とし,これらの間の対応を
| |
|
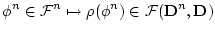 |
|
| |
|
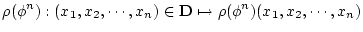 |
(4.46) |
で表す。
- 述語記号と
 上の述語との対応
上の述語との対応
真理値の集合を
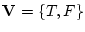 ,
,
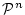 を
を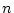 変数の述語記号の全体の集合として,
変数の述語記号の全体の集合として,
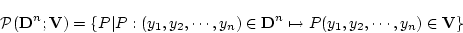 |
(4.47) |
を 上の
上の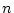 変数の述語全体の集合とする。
変数の述語全体の集合とする。
これらの間の対応を
で表す。
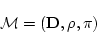 |
(4.49) |
を解釈という。
解釈
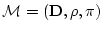 と対象変数記号と
と対象変数記号と の要素
との対応
の要素
との対応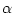 を用いて,項に
を用いて,項に の要素を対応させ,論理式にはその真理値を対応させる作用
の要素を対応させ,論理式にはその真理値を対応させる作用
![$\tau({\cal M},{\bf\alpha})[ \cdot ]$](img747.png) を以下のように帰納的に定める。
を以下のように帰納的に定める。
- 項の値
- 対象変数記号
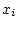 に対しては
に対しては
![\begin{displaymath}
\tau({\cal M},{\bf\alpha})[x_i]=\alpha(x_i)
\end{displaymath}](img748.png) |
(4.50) |
- 対象定数記号
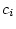 に対しては,これは
に対しては,これは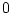 変数の関数
であり,
変数の関数
であり,
![\begin{displaymath}
\tau({\cal M},{\bf\alpha})[c_i]=\rho(c_i)
\end{displaymath}](img750.png) |
(4.51) |
-
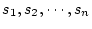 が項で,それぞれ,
が項で,それぞれ,
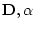 での値が
での値が
![\begin{displaymath}
\tau({\cal M},{\bf\alpha})[s_i],i=1,\cdots,n
\end{displaymath}](img753.png) |
(4.52) |
のとき,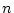 変数関数
変数関数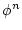 については
については
![\begin{displaymath}
\tau({\cal M},{\bf\alpha})[{\bf\phi}^n(s_1,s_2,\cdots,s_n)...
...M},{\bf\alpha})[s_2],\cdots,\tau({\cal M},{\bf\alpha})[s_n])
\end{displaymath}](img755.png) |
(4.53) |
- 論理式の値
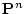 が
が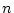 変数の述語変数記号で,
変数の述語変数記号で,
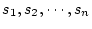 が項のとき,
が項のとき,
![\begin{displaymath}
\tau({\cal M},{\bf\alpha})[{\bf P}^n(s_1,s_2,\cdots,s_n)]
...
...},{\bf\alpha})
[s_2],\cdots,\tau({\cal M},{\bf\alpha})[s_n])
\end{displaymath}](img757.png) |
(4.54) |
- 特に
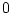 変数の述語記号すなわち命題記号
変数の述語記号すなわち命題記号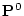 には
には
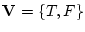 の要素である真理値を
の要素である真理値を
![\begin{displaymath}
\tau({\cal M},{\bf\alpha})[{\bf P}^0]=\pi({\bf P}^0) \in {\bf V}
\end{displaymath}](img759.png) |
(4.55) |
で対応させる。
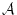 が論理式ならば、
が論理式ならば、
![\begin{displaymath}
\tau({\cal M},{\bf\alpha})[\neg{\cal A}]=\neg \tau[{\cal M},{\bf\alpha}]
({\cal A})
\end{displaymath}](img760.png) |
(4.56) |
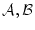 が論理式ならば、
が論理式ならば、
![\begin{displaymath}
\tau({\cal M},{\bf\alpha})[{\cal A} \land {\cal B}]
=\tau(...
...\alpha})[{\cal A}] \land \tau({\cal M},{\bf\alpha})[{\cal B}]
\end{displaymath}](img761.png) |
(4.57) |
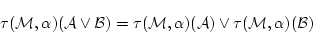 |
(4.58) |
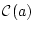 が変数記号
が変数記号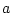 を論理式で,
を論理式で,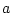 が自由変数記号のとき,
が自由変数記号のとき,
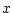 を
を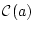 の中に現れない対象変数記号ならば
の中に現れない対象変数記号ならば
![\begin{displaymath}
\tau({\cal M},{\bf\alpha})[(\forall x)({\cal C}(x))]
=\bigwedge_{b \in {\bf D}}\tau({\cal M},{\bf\alpha})[{\cal C}](b)
\end{displaymath}](img763.png) |
(4.59) |
![\begin{displaymath}
\tau({\cal M},{\bf\alpha})[(\exists x)({\cal C}(x) ) ]
=\bigvee_{b \in {\bf D}}\tau({\cal M},{\bf\alpha})[{\cal C}](b)
\end{displaymath}](img764.png) |
(4.60) |
例えば
 が有限集合
が有限集合
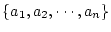 とし,
とし,
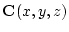 が3変数の述語とする。
が3変数の述語とする。
対象変数記号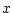 ,対象定数記号
,対象定数記号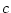 に対して,
に対して,
| |
|
![$\displaystyle \tau({\cal M},{\bf\alpha})[x]=\alpha(x)=a_1$](img768.png) |
|
| |
|
![$\displaystyle \tau({\cal M},{\bf\alpha})[c]=\rho(c)=a_3$](img769.png) |
(4.61) |
とすると



: 充足性とモデル
: 述語論理の公理系
: 演繹定理
Yasunari SHIDAMA
![]() 上の変数を表す対象変数記号,
上の変数を表す対象変数記号, ![]() から
から![]() への関数を表す関数記号および
への関数を表す関数記号および![]() 上の述語を表す述語記号から作られた記号列に過ぎない。
上の述語を表す述語記号から作られた記号列に過ぎない。
![]() と対象変数記号と
と対象変数記号と![]() の要素
との対応
の要素
との対応![]() を用いて,項に
を用いて,項に![]() の要素を対応させ,論理式にはその真理値を対応させる作用
の要素を対応させ,論理式にはその真理値を対応させる作用
![]() を以下のように帰納的に定める。
を以下のように帰納的に定める。
![\begin{displaymath}
\tau({\cal M},{\bf\alpha})[(\forall x)({\cal C}(x))]
=\bigwedge_{b \in {\bf D}}\tau({\cal M},{\bf\alpha})[{\cal C}](b)
\end{displaymath}](img763.png)
![\begin{displaymath}
\tau({\cal M},{\bf\alpha})[(\exists x)({\cal C}(x) ) ]
=\bigvee_{b \in {\bf D}}\tau({\cal M},{\bf\alpha})[{\cal C}](b)
\end{displaymath}](img764.png)
![]() ,対象定数記号
,対象定数記号![]() に対して,
に対して,
![$\displaystyle \tau({\cal M},{\bf\alpha})[(\forall z)({\cal C}(x,c,z)) ]
=\bigwedge_{b \in {\bf D}}\tau({\cal M},{\bf\alpha})[{\cal C}(x,c,b))]$](img770.png)
![$\displaystyle =\bigwedge_{b \in {\bf D}}\pi({\cal C})(\tau({\cal M},{\bf\alpha})[x],
\tau({\cal M},{\bf\alpha})[c],b)$](img771.png)
![$\displaystyle \tau({\cal M},{\bf\alpha})[(\exists z)({\cal C}(x,c,z)) ]
=\bigvee_{b \in {\bf D}}\tau({\cal M},{\bf\alpha})[{\cal C}(x,c,b))]$](img773.png)
![$\displaystyle =\bigvee_{b \in {\bf D}}\pi({\cal C})(\tau({\cal M},{\bf\alpha})[x],
\tau({\cal M},{\bf\alpha})[c],b)$](img774.png)