


: スコーレム標準形
: 導出原理
: 導出原理
この章では個体閉論理式
から
論理式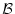 を導出原理を用いて証明する方法を説明する。
を導出原理を用いて証明する方法を説明する。
体系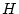 の公理系に論理式
の公理系に論理式
を追加してできる新たな系で
論理式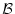 が証明可能であるとき,このことを
が証明可能であるとき,このことを
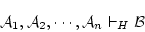 |
(5.1) |
で表した。このとき演繹定理によれば,
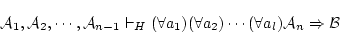 |
(5.2) |
が成り立つ。
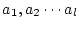 は
は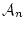 に現れる総ての自由変数記号
とする。
に現れる総ての自由変数記号
とする。
特に
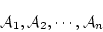 |
(5.3) |
が自由変数を持たない個体閉論理式の集合であれば,全称記号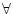 の作用は
無効になるから
の作用は
無効になるから
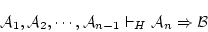 |
(5.4) |
であり,これと公理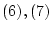
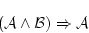 |
(5.5) |
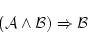 |
(5.6) |
を繰り返し用いて,
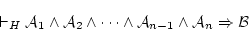 |
(5.7) |
上の議論の逆を辿れば,結局,
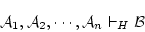 |
(5.8) |
が成立つのは
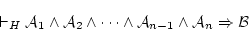 |
(5.9) |
が成立つとき,かつそのときに限る。
完全性定理によれば,後者は,
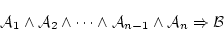 |
(5.10) |
が恒真論理式であることに等しい。
これはこの論理式の否定
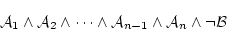 |
(5.11) |
が恒偽論理式であること,すなわち充足不能であることと同じである。



: スコーレム標準形
: 導出原理
: 導出原理
Yasunari SHIDAMA
![]() の公理系に論理式
の公理系に論理式